Está dictado por un conjunto de inecuaciones, donde todas tienen propiedad lineal sobre el planteamiento de las mismas incógnitas, de modo que encontrar una solución consiste en dar un valor a cada variable conforme el cumplimiento de las inecuaciones presentes.
Explicación de las condiciones
Por ejemplo, una empresa de chocolates produce dos tipos de barras: una simple y una especial rellena, disponible en cajas que contienen 6 items de cada clase. Cada barra simple se vende a $55 y los especiales a $85. Los costos de producción por unidad son de $30 y $50 respectivamente. Por mes debe ganar con la venta de ambos tipo de productos un mínimo de $20000 y los costos de producción no deben superar los $10000. El dueño de la empresa quiere saber cuántas barras de cada tipo conviene fabricar por mes para que la empresa obtenga ganancias.
Si se define x como la cantidad de barras simples e y como la cantidad de barras especiales, el problema se puede representar a través del siguiente sistema de inecuaciones:
\(\left\{ \begin{align}
& 0\le x \\
& 0\le y \\
& 55x+85y\ge 20000 \\
& 30x+50y\le 10000 \\
\end{align} \right.\)
Las distintas inecuaciones expresan cada una de las condiciones que se deben cumplir al mismo tiempo.
Hallar la solución de este sistema es encontrar el conjunto de puntos en el plano en el cual se cumplen todas las restricciones. Este conjunto de puntos se denomina conjunto solución o región factible.
Entonces, a continuación, se representa el conjunto de puntos del plano que satisfacen todas las restricciones:
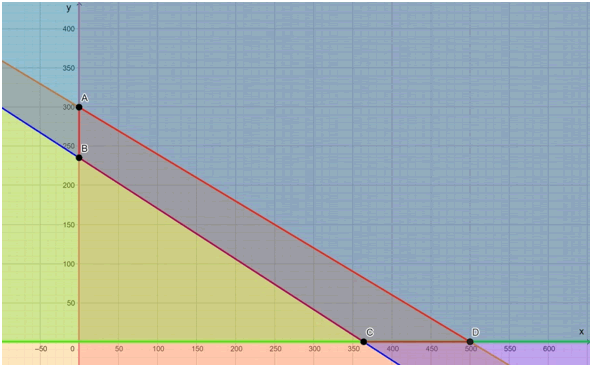
Como se puede observar en la imagen, se marcó con rosado la región correspondiente a la primera restricción, con verde la región de la segunda expresión, con azul la que corresponde a la tercera restricción y, por último, con naranja la última expresión.
Por lo tanto, el conjunto solución o región factible es el conjunto de los puntos en el plano que se forma con los cuatro colores y se puede observar que es un polígono convexo, más precisamente, un cuadrilátero.
Si un sistema de inecuaciones lineales tiene una incógnita, la solución puede ser un punto, el conjunto vacío o infinitos puntos.
En cambio, si tiene dos incógnitas, la solución es la intersección de semiplanos que puede ser vacía o un subconjunto del plano.
Dado el sistema de inecuaciones lineales con dos incógnitas: \(4x-3y>16\). Se quiere hallar el punto \(\left( x,y \right)\) tal que \(4x-3y>16\).
Entonces, se puede escribir
\(y<\frac{4x-16}{3}\)
Se sabe que los puntos \(\left( x,y \right)\) que satisfacen la igualdad \(y=\frac{4x-16}{3}\) son los que están en la siguiente recta:
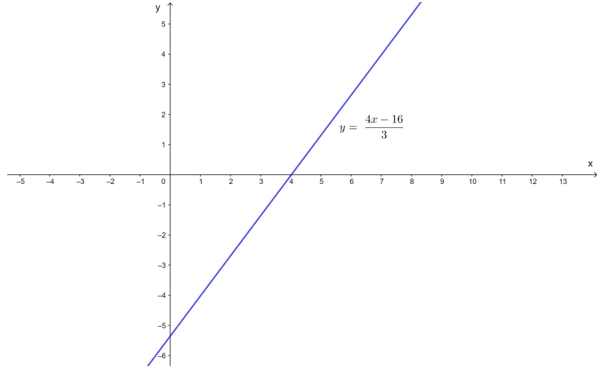
Esto es, dado cualquier valor de x, el punto \(R=\left( x,y \right)\) que está en la recta, satisface la igualdad \(y=\frac{4x-16}{3}\).
Luego, para ese mismo valor de x, un punto \(\left( x,y \right)\) que cumple que \(y<\frac{4x-16}{3}\), estará debajo de R.
Por tanto, para todos los valores de x, tenemos la solución:
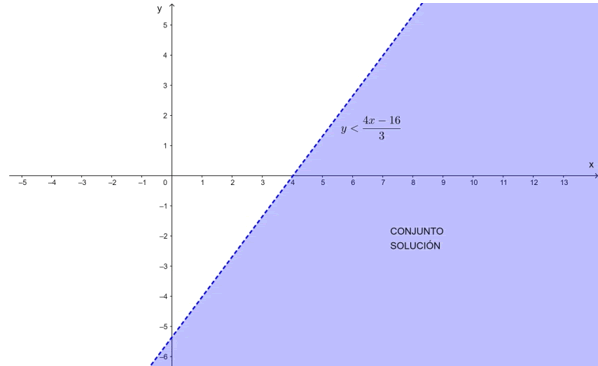
Como se puede ver en el gráfico, la solución es el semiplano que abarca todos los puntos por debajo de la recta frontera \(y=\frac{4x-16}{3}\). Al no incluir los puntos de la recta, se dice que el semiplano es abierto.
Ahora, se quiere hallar la solución del sistema de inecuaciones:
\[\left\{ \begin{align}
& 4y+2x\le 16 \\
& y+5x\le 25 \\
& x\ge 0 \\
& y\ge 0 \\
\end{align} \right.\]
Se representan las cuatro inecuaciones en los siguientes gráficos:
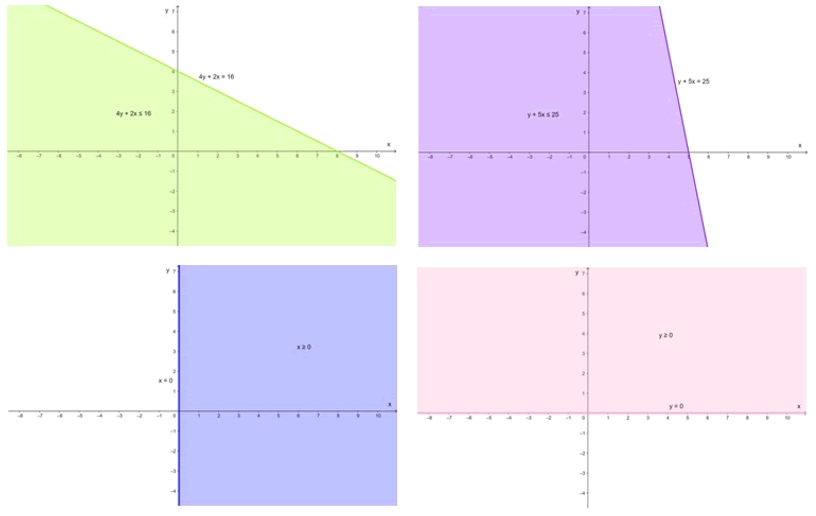
Por tanto, el conjunto solución de este sistema es la intersección de los cuatro semiplanos cerrados. Representado gráficamente, la solución es el polígono que se observa:
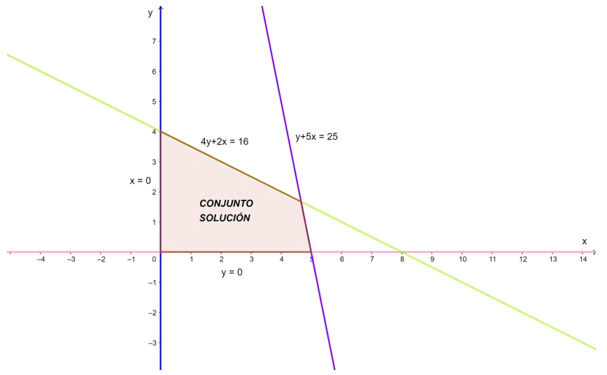
A continuación, se presenta el sistema de inecuaciones lineales:
\(\left\{ \begin{align}
& 5x-10y<20 \\
& y-6x>12 \\
\end{align} \right.\)
Si se representa gráficamente, se observa lo siguiente:
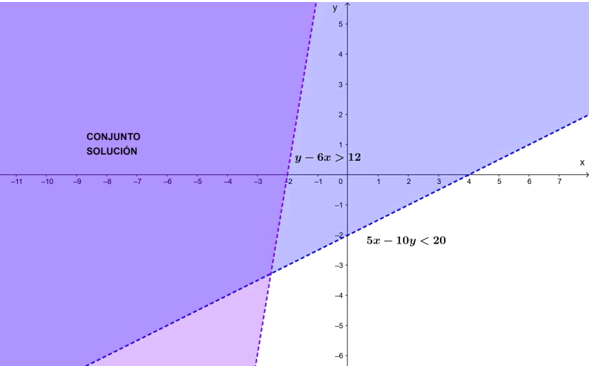
Por tanto, la solución del sistema es la parte más oscura que se observa en la gráfica. En este caso, la solución es un conjunto no acotado.
Por último, se pueden combinar desigualdades estrictas como no estrictas en un sistema de inecuaciones lineales:
\[\left\{ \begin{align}
& 6y-2x\ge 16 \\
& 6y-2x<8 \\
\end{align} \right.\]
Gráficamente, se observa lo siguiente:
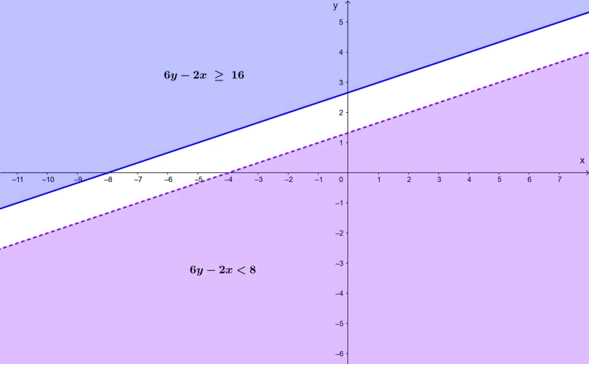
En este caso, la intersección de las regiones factibles es vacía y, en consecuencia, el conjunto solución también es vacío, esto es, no hay puntos en el plano que satisfagan el sistema de inecuaciones anterior.
Autora
Escrito por Regina Meyer para la Edición #104 de Enciclopedia Asigna, en 09/2021. Regina es Licenciada en Matemática Aplicada, con especialización en Problemas de Optimización, y experiencia en calidad de Docente Universitaria así como también en el nivel Secundario.