Una inecuación es una desigualdad que involucra una(s) incógnita(s). Por desigualdad se entiende que las expresiones deben tener uno de los siguientes signos: > (mayor), ≥ (mayor o igual), < (menor), ≤ (menor o igual).
Notar que los símbolos que no tienen el trazo-guion debajo del “pico” se llaman desigualdades estrictas y las que la tienen se denominan desigualdades no estrictas. Por su parte, estos signos actúan como separadores entre el primer miembro (ubicado a la izquierda), y el segundo miembro (a la derecha), que se plantean en la inecuación.
Resolver una inecuación consiste en encontrar los valores de las incógnitas que hacen que se satisfaga la inecuación, esto es, se cumpla la desigualdad.
OBSERVACIÓN: Siempre verificar el resultado al resolver una inecuación. ¿Cómo se hace? Se reemplaza el/los valores obtenidos para la incógnita en la inecuación, se calcula y comprueba si se cumple la desigualdad.
Ejemplos de inecuaciones
a) \(3x+2\le {{x}^{2}}+4\)
b) \(\left| {2x+3} \right|>-3x+2\)
c) \(\frac{{4{{x}^{4}}+2}}{{\left( {x-1} \right)\left( {2x+1} \right)}}\ge 0\)
d) \({{x}^{2}}-3x<{{x}^{5}}-3\).
En las inecuaciones generalmente hay varias soluciones que pueden ser puntos aislados o intervalos de números reales, dependiendo del dominio de las incógnitas.
Para resolver una inecuación se procede de manera similar a lo que se hace con una ecuación, realizar la misma operación en ambos términos de la desigualdad. Por ejemplo, para encontrar las soluciones de la inecuación \(-4x+2\ge 3\) se procede de la siguiente manera:
\(-4x+2\ge 3\Leftrightarrow -4x+2-2\ge 3-2\Leftrightarrow -4x\ge 1\Leftrightarrow \frac{{-4x}}{{-4}}\le \frac{1}{{-4}}\Leftrightarrow x\le -\frac{1}{4}\)
Así, el conjunto solución es \(S=\left\{ {x\in \Re :x\le -\frac{1}{4}} \right\}\), el cual se puede escribir de forma equivalente como el intervalo \(\left( {-\infty ,-\frac{1}{4}} \right]\). Gráficamente, en la recta numérica, se visualiza de esta manera:
Verificación: Para verificar que el conjunto solución es el correcto, se toma un valor cualquiera igual o menor que \(-\frac{1}{4}\) :
\(-4.-2+2=8+2=10>3\). Se verifica.
OBSERVACIÓN: Cuando se resuelve una inecuación como la anterior se dice que el 2 “pasa restando al miembro derecho” y se escribe directamente \(-4x\ge 3-2\). Es correcto omitir el paso anterior y el resultado que se obtiene es correcto, pero es preciso recordar que no existe el “pasaje de términos”, lo que se hace en realidad es operar en ambos miembros de la inecuación.
Cabe destacar que multiplicar ambos miembros por un número negativo invierte la desigualdad.
Una inecuación de este estilo: \(\left| {2x-6} \right|<3\) se resuelve de la siguiente forma:
\(\left| {2x-6} \right| < 3\Leftrightarrow -\left( 3 \right) < 2x-6 < 3\Leftrightarrow -3 < 2x-6 < 3\Leftrightarrow -3+6 < 2x-6+6 < 3+6\Leftrightarrow 3 < 2x < 9\)
\(\Leftrightarrow \frac{3}{2}<\frac{{2x}}{2}<\frac{9}{2}\Leftrightarrow \frac{3}{2} Verificación: En este caso, se toma un valor cualquiera mayor que \(\frac{3}{2}\) y menor que \(\frac{9}{2}\) : \(\left| {2.2-6} \right|=\left| {4-6} \right|=\left| {-2} \right|=2\) y \(2\in \left( {\frac{3}{2},\frac{9}{2}} \right)\) por tanto, se verifica. Hay inecuaciones en las que las soluciones están unidas con un “o” como es el caso de la inecuación \({{\left( {x-4} \right)}^{2}}\ge 144\) que se resuelve de la siguiente manera: \(\left| 2x-6 \right|<3\Leftrightarrow -\left( 3 \right)<2x-6<3\Leftrightarrow -3<2x-6<3\Leftrightarrow -3+6<2x-6+6<3+6\Leftrightarrow 3<2x<9\)
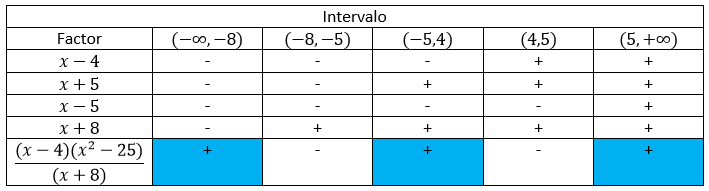
\(\Leftrightarrow \frac{3}{2}<\frac{2x}{2}<\frac{9}{2}\Leftrightarrow \frac{3}{2} Verificación: Para proceder a la validación se toma un valor cualquiera igual o menor que -8 y un número cualquiera mayor o igual a 16: \({{\left( {-10-4} \right)}^{2}}={{\left( {-14} \right)}^{2}}=196>144\). Se verifica. \({{\left( {20-4} \right)}^{2}}={{\left( {16} \right)}^{2}}=256>144\). Se verifica. Por último, se considera, por ejemplo, la siguiente inecuación: \(\frac{{\left( {x-4} \right)\left( {{{x}^{2}}-25} \right)}}{{\left( {x+8} \right)}}\ge 0\). Se plantea la siguiente tabla: Luego, por la tabla se ve que el conjunto solución es \(S=\left\{ {x\in \Re :x<-8\wedge -5\le x\le 4\wedge 5\le x} \right\}\) o lo que es equivalente \(S=\left( {-\infty ,-8} \right)\cup \left[ {-5,4} \right]\cup \left[ {5,+\infty } \right)\).
Gráficamente,
Verificación: Para la correspondiente comprobación, se toma un valor cualquiera menor que -8, otro entre -5 y 4 (pueden ser los extremos) y un número cualquiera mayor o igual a 5: \(\frac{{\left( {-12-4} \right)\left( {{{{\left( {-12} \right)}}^{2}}-25} \right)}}{{\left( {-12+8} \right)}}=\frac{{-16.\left( {144-25} \right)}}{{-4}}=\frac{{-1904}}{{-4}}=476>0\). Se verifica. \(\frac{{\left( {4-4} \right)\left( {{{4}^{2}}-25} \right)}}{{\left( {4+8} \right)}}=\frac{{0.\left( {16-25} \right)}}{{12}}=0\). Se verifica. \(\frac{{\left( {10-4} \right)\left( {{{{10}}^{2}}-25} \right)}}{{\left( {10+8} \right)}}=\frac{{6.\left( {100-25} \right)}}{{18}}=\frac{{450}}{{18}}=25>0\). Se verifica.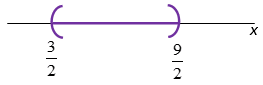
Autora
Escrito por Regina Meyer para la Edición #103 de Enciclopedia Asigna, en 08/2021. Regina es Licenciada en Matemática Aplicada, con especialización en Problemas de Optimización, y experiencia en calidad de Docente Universitaria así como también en el nivel Secundario.