Primeramente, una ecuación lineal es una expresión asociada a operaciones básicas (suma, resta, multiplicación y división) respecto de una(s) incógnita(s) las cuales no aparecen multiplicándose o dividiéndose entre sí. En este caso, también se dice que se trata de una ecuación de primer grado. De este modo, quedan excluidas, por ejemplo, operaciones exponenciales (a no ser a la primera potencia) o de radicación. Por lo tanto, un sistema de ecuaciones lineales está constituido por un grupo de ecuaciones lineales, cuya resolución implica proporcionar un valor concreto para cada variable de modo que se cumplan todas las ecuaciones.
Sistemas de dos ecuaciones lineales (y dos incógnitas)
A continuación se analizará en detalle los sistemas de dos ecuaciones lineales con dos incógnitas, cuya forma general es:
a11x + a12 y = b1
a21 x + a22y = b2
donde x e y son las incógnitas mientras que a11,a12,a21,a22,b1 y b2 son números reales. La solución es un punto (x,y) que satisfacepppp las dos ecuaciones.
Ejemplos e interpretación geométrica de los sistemas de dos ecuaciones lineales
Este tipo de sistemas surge de forma natural al trabajar con rectas en el plano, ya que cada ecuación lineal es una recta. Todos los puntos de esa recta son soluciones de la ecuación y viceversa. Entonces, si tenemos dos rectas, se genera un sistema con dos ecuaciones. Si las rectas se cortan en un punto, ese punto pertenece a ambas rectas, es decir, es solución de ambas ecuaciones o lo que es lo mismo, es solución del sistema de ecuaciones.
Desde este punto de vista geométrico, es claro que sólo pueden ocurrir tres situaciones:
A) Sistema Compatible Determinado: las rectas se cortan en un único punto y por lo tanto el sistema tiene solución única;
B) Sistema Compatible Indeterminado: se tiene dos veces la misma recta y en ese caso todos sus puntos son solución del sistema, es decir hay infinitas soluciones;
C) Sistema Incompatible: las rectas son paralelas y no se cortan, en ese caso el sistema no tiene solución.
Sistema compatible: solución única
Se considera,
2x – y = 4
x + y = 6
Las ecuaciones corresponden a las rectas representadas en el siguiente gráfico. La solución del sistema se encuentra en la intersección de las dos rectas:
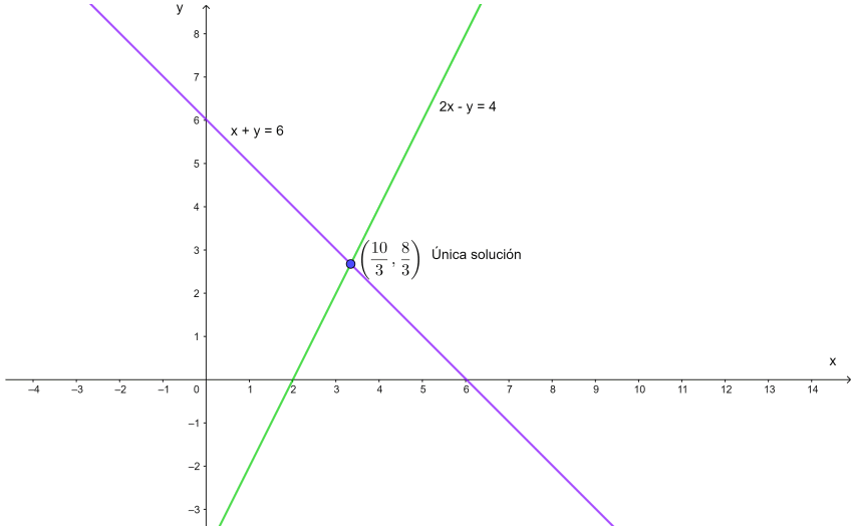
Analíticamente la solución se encuentra de la siguiente manera: de la segunda ecuación se tiene que y = 6 – x.
Reemplazando esto en la primera ecuación: 2x – (6 – x) = 4,
de lo cual se sigue que
\(x=~\frac{10}{3}\).
Luego, volviendo a la expresión para el valor de y en función de x, se tiene que
\(y=6-\frac{10}{3}=\frac{8}{3}\),
es decir, la solución al sistema es el punto
\(\left( \frac{10}{3},\frac{8}{3} \right)\).
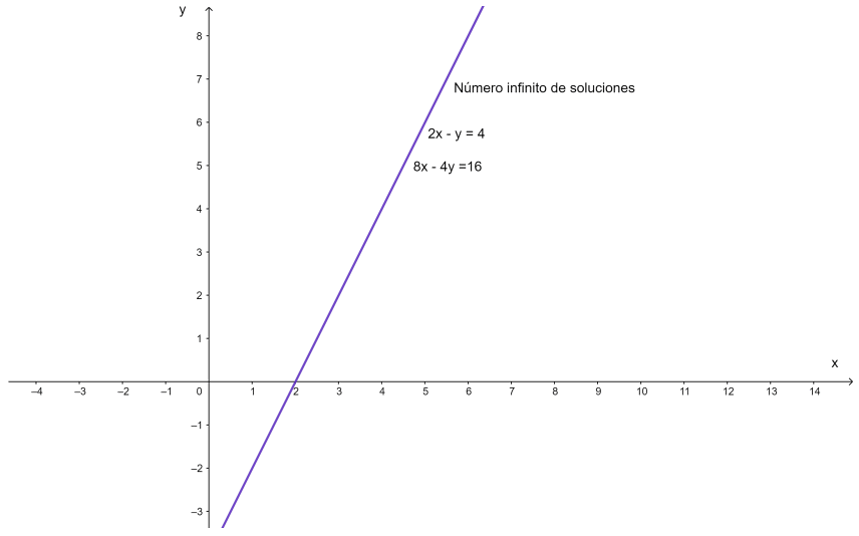
Sistema Compatible Indeterminado: número infinito de soluciones
Dado el sistema,
2x – y = 4
8x – 4y = 16
Como se puede observar, estas dos ecuaciones son equivalentes, multiplicando la primera ecuación por 4 obtenemos la segunda, o viceversa, dividiendo la segunda ecuación por 4 se tiene la primera ecuación. Ambas ecuaciones representan la misma recta, todos los puntos de la misma son solución del sistema. Las infinitas soluciones se pueden escribir de la forma (x,y) = (x,2x – 4) donde x es un número real cualquiera.
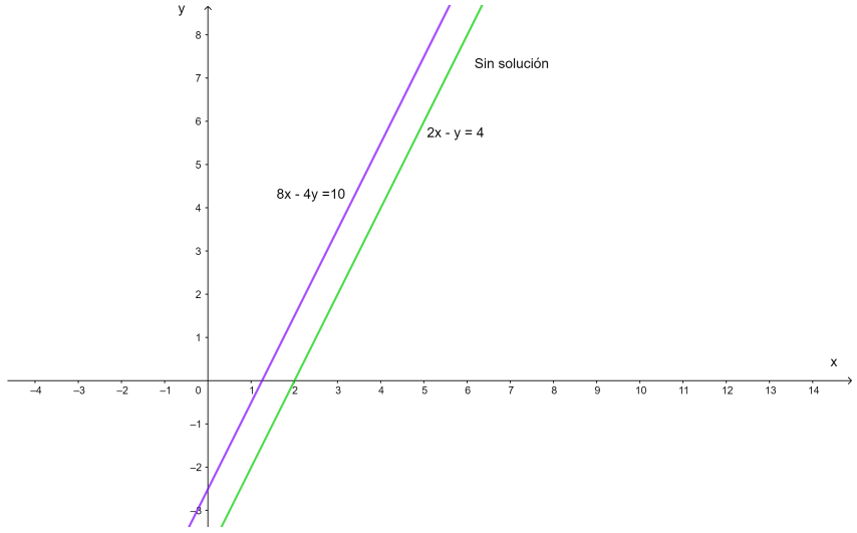
Sistema Incompatible: sin solución:
Se considera,
2x – y = 4
8x – 4y = 10
Este sistema corresponde a dos rectas paralelas y distintas, por tanto no hay un punto de intersección entre las mismas, es decir, no hay solución al sistema de ecuaciones:
Ejercicio al respecto de una situación cotidiana
Supongamos que nos enfrentamos a la siguiente situación: una persona compra 100 kilos de harina común y 50 kilos de harina refinada. Sabe que la harina refinada es un 30% más cara que la común y el monto total de la compra fue de $8250. Quiere averiguar cuál es el precio por kilo de cada tipo de harina.
Si se definen x e y como el precio por kilo de la harina común y refinada respectivamente, la situación se puede representar de la siguiente manera:
100x + 50y = 8250
y = 1,3x
que es un sistema de dos ecuaciones lineales con dos incógnitas.
Para resolverlo se reemplaza y = 1,3x en la primera ecuación y se obtiene: 100x + 50 (1,3x) = 8250, a partir de lo cual x = 50, y luego, y = 1,3 * 50 = 65. Es decir, el kilo de harina común cuesta $50 mientras que la refinada $65.
Autora
Escrito por Regina Meyer para la Edición #102 de Enciclopedia Asigna, en 08/2021. Regina es Licenciada en Matemática Aplicada, con especialización en Problemas de Optimización, y experiencia en calidad de Docente Universitaria así como también en el nivel Secundario.