Definición
La Ley de Gauss constituye una de las ecuaciones de Maxwell, la cual permite relacionar el campo eléctrico con su fuente, es decir, con la carga eléctrica, a partir de la relación que existe entre el flujo eléctrico a través de una superficie cerrada y la carga neta encerrada dentro de dicha superficie. Para poder aplicar la Ley de Gauss es necesario conocer previamente la dirección y el sentido de las líneas de campo eléctrico generadas por la distribución de carga.
La Ley de Gauss es una alternativa a la Ley de Coulomb, formulada en el año 1835 por el matemático, astrónomo y físico alemán Johann Carl Friederich Gauss (1777-1855), el cual es considerado como uno de los más grandes matemáticos de todos los tiempos.
La Ley de Gauss establece que “el flujo eléctrico dada mediante una superficie cerrada equivale a la carga neta encerrada por la superficie dividida por la constante dieléctrica del medio (\({{\varepsilon }_{0}}\))”.
\({{\text{ }\!\!\Phi\!\!\text{ }}_{E}}=~\frac{{{Q}_{n}}}{{{\varepsilon }_{0}}}\)
Utilizando la definición de flujo eléctrico, la ecuación anterior se puede escribir como:
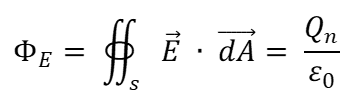
Donde:
\({{\text{ }\!\!\Phi\!\!\text{ }}_{E}}\): flujo eléctrico a través de la superficie
\(\vec{E}\): vector campo eléctrico.
\(\overrightarrow{dA}\) : vector diferencial de área (siempre perpendicular a la superficie y saliendo de ésta).
\({{Q}_{n}}\) : carga neta encerrada por la superficie.
\({{\varepsilon }_{0}}~\) : Constante de permitividad del medio. En la mayoría de los casos el medio es el vacío o espacio libre, donde
De este modo, si se conoce la carga neta encerrada por la superficie, es posible calcular, utilizando la Ley de Gauss, el campo eléctrico generado por dicha carga eléctrica.
La superficie cerrada que se utiliza para aplicar la Ley de Gauss, es una superficie imaginaria, conocida como superficie gaussiana.
Cuando la carga eléctrica neta encerrada por la superficie es cero, el flujo eléctrico neto a través de dicha superficie gaussiana debe ser nulo, aunque algunas partes de la superficie tengan flujo positivo (líneas de campo eléctrico saliendo) y otras tengan flujo negativo (líneas de campo eléctrico entrando).
Condiciones para aplicar la Ley de Gauss
• El campo eléctrico sobre la superficie gaussiana debe ser constante.
• Debe existir simetría esférica, cilíndrica o cartesiana (plana).
• El ángulo entre el \(\overrightarrow{dA}\) y el \(\vec{E}\) debe ser constante a lo largo de toda la superficie.
• La superficie gaussiana a utilizar se elige de acuerdo a la simetría del problema.
Ejemplo práctico: Calcule el campo eléctrico generado por una carga puntual positiva a una distancia R de la misma
Una carga puntual positiva genera líneas de campo eléctrico radiales y alejándose de la carga, por la simetría del problema, la superficie gaussina que se emplea es una esfera, cuyo centro estará ubicado en la carga. El diferencial de área (\(\overrightarrow{dA}\)) es perpendicular a la superficie de la esfera (paralelo al \(\vec{E}\)) y saliendo de ella.
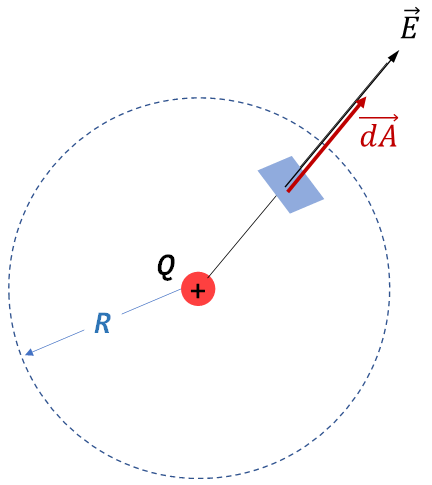
Sabemos por definición que:
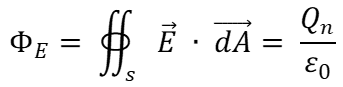
Como se conoce la carga neta dentro de la superficie y deseamos calcular el campo eléctrico:
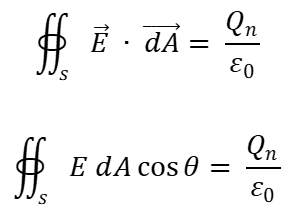
Como el campo eléctrico es constante en cualquier punto de la superficie y el ángulo \(\theta \) entre \(\vec{E}\) y \(\overrightarrow{dA}\) es igual a 0° (\(\cos 0{}^\circ =1\)), se tiene que:
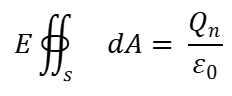
Donde:
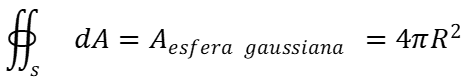
Por lo tanto:
\(E=~\frac{{{Q}_{n}}}{4\pi {{R}^{2}}{{\varepsilon }_{0}}}\)
Este valor de campo eléctrico es el mismo que se obtiene a partir de la Ley de Coulomb para un punto P cualquiera ubicado a una distancia R de una carga puntual.
Ejemplos de las aplicaciones de la Ley de Gauss
Como ya se mencionó anteriormente, la Ley de Gauss es una alternativa a la Ley de Coulomb, que se aplica en determinadas ocasiones, donde, de acuerdo a la simetría de la carga, resulta más sencillo calcular el campo eléctrico aplicando la Ley de Gauss que la Ley de Coulomb.
La ley de Gauss es muy útil para determinar el campo eléctrico en situaciones de alta simetría tales como el campo eléctrico generado por una:
• Carga puntual
• Distribución de carga sobre un plano infinito.
• Línea de carga infinita.
• Esfera maciza cargada.
• Cascarón esférico.
• Superficie cilíndrica infinita.
• Cilindro macizo de longitud infinita.
Cuando se va a aplicar la Ley de Gauss para determinar el campo eléctrico de una distribución de carga, es necesario conocer si se trata de un material aislante o de un material conductor, ya que el comportamiento de la carga en ambos materiales es totalmente diferente.
Si se trata de un material aislante, la carga puede estar distribuida de forma uniforme o no uniforme en el mismo, dependiendo de si su densidad de carga lineal (λ), superficial (σ) o volumétrica (ρ), es constante o varia de acuerdo a una función dada.
Por el contrario, si se trata de un material conductor la carga en el mismo cumple con las siguientes condiciones de un conductor en equilibrio electrostático (conductor en el cual no hay movimiento neto de carga en su interior):
• El campo eléctrico en cualquier punto interior del conductor es cero.
• El campo eléctrico en la superficie externa de un conductor cargado tiene una dirección perpendicular a dicha superficie y una magnitud de \({}^{\sigma }\!\!\diagup\!\!{}_{{{\varepsilon }_{0}}}\;\), donde σ representa la carga por unidad de área en ese punto del conductor.
• Toda carga eléctrica en un conductor aislado residirá en su superficie.
• En un conductor de forma irregular, la carga eléctrica tenderá a acumularse en los puntos afilados, es decir, en aquellos puntos de la superficie de menor radio de curvatura.
Autora
Escrito por Lismarihen Larreal para la Edición #106 de Enciclopedia Asigna, en 12/2021. Lismarihen es Ingeniera Mecánica, con maestría en Física Aplicada y doctorado en Ingeniería Ambiental, asímismo se desempeña como Docente e Investigadora en el Depto. de Física de la Facultad de Ingeniería de la Universidad del Zulia.