La intersección entre un elemento geométrico y otro consiste en los puntos que tienen en común. Por ejemplo, dos rectas no paralelas sobre un mismo plano, se cortan en un punto único, pero la intersección entre dos superficies puede ser una curva, y entre dos volúmenes, una superficie.
Dos planos, como el del suelo de una habitación y una pared perpendicular a él, tienen por intersección una línea recta, claramente visible. Asimismo, las trayectorias de dos móviles podrían intersectarse en algún punto, como por ejemplo una pelota lanzada verticalmente hacia arriba y otra proyectada horizontalmente.
En cualquier caso, para determinar de forma analítica los puntos de intersección entre los elementos, es necesario conocer la ecuación que representa a cada uno e igualarlas, lo que da lugar a una o varias ecuaciones. La solución de estas es la intersección buscada, como se muestra en los siguientes ejemplos.
1. Intersección de una curva con los ejes coordenados
La intersección o puntos de corte entre una curva y los ejes coordenados, brinda importante información respecto al comportamiento de la gráfica.
Para encontrar los puntos de corte respectivos se procede de esta forma:
• Eje vertical, sustituir x = 0 y resolver la ecuación obtenida.
• Eje horizontal, se hace y = 0 y se resuelve la ecuación resultante.
La intersección corresponde a los puntos solución. Si no existen, la curva carece de intersección con el eje en cuestión.
Ejemplo
Determinar las intersecciones con los ejes coordenados de la parábola dada por:
\(y=-2{{x}^{2}}+x+3\)
Para x = 0
\(y=3\)
La intersección con el eje vertical es el punto (0;3).
Para y = 0
\(-2{{x}^{2}}+x+3=0\)
Es una ecuación de segundo grado, que se resuelve a través de la fórmula cuadrática:
\(x=\frac{{-b\pm \sqrt{{{{b}^{2}}-4ac}}}}{{2a}}\)
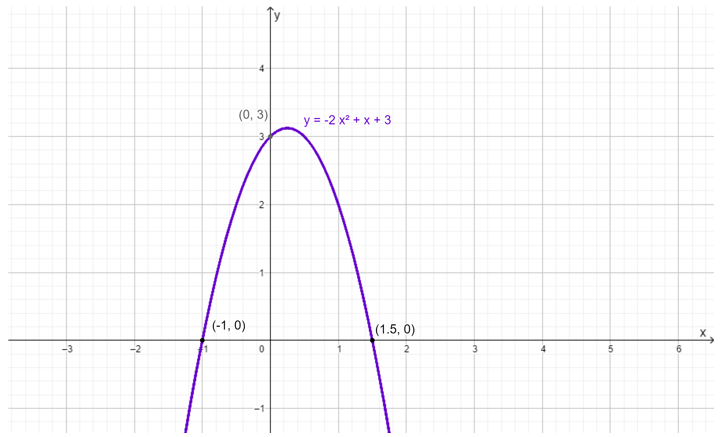
Con a = −2; b = 1 y c = 3. La ecuación tiene dos soluciones: x1 = −1 y x2 = 3/2 = 1.5, por lo tanto, la parábola tiene dos intersecciones con el eje x, los puntos (−1,0) y (1.5;0).
La gráfica, con sus respectivas intersecciones, se muestran en la siguiente figura:
2. Intersección entre dos rectas
Dos rectas no paralelas en un mismo plano tienen un punto de intersección. Si se conocen las ecuaciones de las rectas, simplemente se igualan para hallar el punto en común, mediante la solución de la ecuación lineal así obtenida.
Sean las rectas L1 y L2, dadas por: \(y={{m}_{1}}x+{{b}_{1}}\) y \(y={{m}_{2}}x+{{b}_{2}}\). Igualando ambas ecuaciones, se obtiene el punto P (xo, yo), que satisface simultáneamente a ambas.
Ejemplo
Para encontrar la intersección entre las rectas: \(y=4x-1\) y \(y=-2x+5\), se igualan ambas ecuaciones:
\(4x-1=-2x+5\)
\(4x+2x=5+1\)
Obtenido el valor de x, común a ambas rectas, se sustituye en cualquiera de ellas para obtener el valor de y. Por ejemplo, sustituyendo x = 1 en L1:
La intersección buscada es el punto (1,3).
3. Intersección entre dos curvas
La forma de hallar la intersección entre dos curvas, es semejante a la descrita en el ejemplo de las dos rectas.
Ejemplo
Hallar, si los hay, los puntos en que se intersectan las siguientes curvas:
\(y=-{{x}^{2}}\) , \(y=2{{x}^{2}}-1\)
Se igualan ambas ecuaciones:
\(-{{x}^{2}}=2{{x}^{2}}-1\)
\(x=\pm \sqrt{{\frac{1}{3}}}\)
Hay dos puntos de intersección, uno por cada valor de x obtenido:
\({{y}_{1}}=-{{\left( {\sqrt{{\frac{1}{3}}}} \right)}^{2}}=-\frac{1}{3}\)
\({{y}_{2}}=-{{\left( {-\sqrt{{\frac{1}{3}}}} \right)}^{2}}=-\frac{1}{3}\)
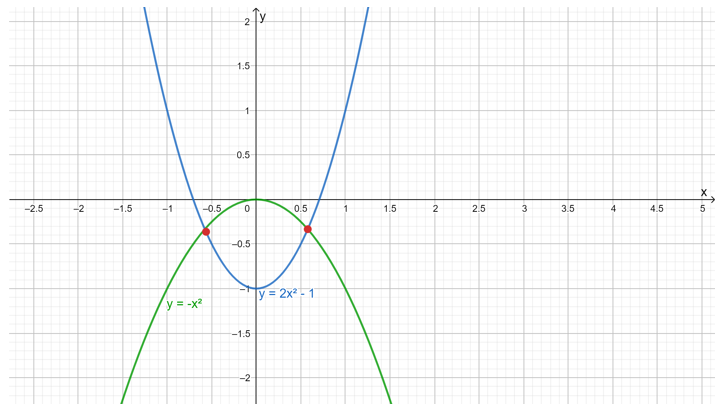
Los puntos de intersección son:
\({{P}_{1}}=~\left( {\sqrt{{\frac{1}{3}}},-\frac{1}{3}} \right)\)
\({{P}_{2}}=~\left( {-\sqrt{{\frac{1}{3}}},-\frac{1}{3}} \right)\)
En la gráfica se muestran estas intersecciones:
4. Intersección entre planos
Consiste en un conjunto de puntos que es común a los planos. Entre dos planos, la intersección, si existe, es una recta, pero también puede ocurrir que los planos no tengan intersección o que, por el contrario, los planos sean enteramente coincidentes.
Para tres planos, la intersección también puede consistir en un punto o una recta, o puede que simplemente no haya puntos de coincidencia entre los tres.
Al determinar analíticamente la intersección entre planos, hay que partir de la ecuación cartesiana de cada uno. De esta manera se forma un sistema de ecuaciones lineales, cuya solución equivale a la intersección buscada.
Ejemplo
Sean dos planos P1 y P2, cuyas respectivas ecuaciones son:
\({{P}_{1}}:~~~~~~~\frac{3}{4}x+2y+2z=5\)
\({{P}_{2}}:~~~~~\frac{3}{4}x-2y+2z=3\)
Al sumar las dos ecuaciones se obtiene:
Y al restarlas:
\(y=\frac{1}{2}\)
Las rectas en el espacio suelen expresarse en términos de un vector llamado “vector director”, que señala su dirección. También hace falta un punto P que pertenezca a la recta, el cual se puede determinar haciendo x = 0, y = 1/2 en las ecuaciones de los planos. De esta manera se halla el correspondiente valor de z:
Si se prefiere el segundo plano, evidentemente se obtiene el mismo valor:
De esta forma se obtiene P (0, ½,2). El siguiente paso es determinar el vector director, a través del producto vectorial entre los vectores normales a los planos. Estos son muy fáciles de encontrar, ya que se forman con los respectivos coeficientes de las variables x, y, z. Se denotan como \({{\vec{n}}_{1}}~\) y \({{\vec{n}}_{2}}\), y en este ejemplo son:
\({{\vec{n}}_{1}}=0.75;2;2\)
\({{\vec{n}}_{2}}=0.75;-2;2\)
Su producto vectorial es:
\({{\vec{n}}_{1}}\times {{\vec{n}}_{2}}=\left| {\begin{array}{*{20}{c}} i & j & k \\ {0.75} & 2 & 2 \\ {0.75} & {-2} & 2 \end{array}} \right|=\left( {4i+1.5j-1.5k} \right)-\left( {1.5k-4i+1.5j} \right)=8i+0j-3k\)
El vector \(i+0j-\frac{3}{8}k\) también es múltiplo de \({{\vec{n}}_{1}}\times {{\vec{n}}_{2}}=8i+0j-3k\), por lo que la recta buscada finalmente se puede expresar como:
\(L = (0, ½,2) + λ \cdot (1, 0,-3/8)\)
Donde λ es el parámetro de la recta.
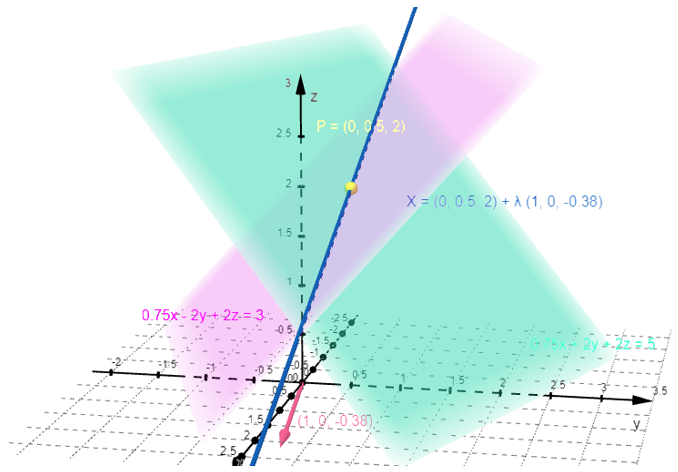
Todo se muestra en la siguiente imagen, en la cual aparecen:
• Los dos planos (turquesa y rosa).
• El punto P (amarillo)
• La recta intersección (azul)
• El vector director de la recta, en la parte inferior del gráfico.
