El tiro horizontal es la atribución de la velocidad horizontal a un objeto sobre una altura en particular, cuyo movimiento continúa de forma natural a efectos de la gravedad, configurando un arco de parábola con su descenso.
Se trata de un movimiento en el plano, en cuya descripción participan ambos ejes de propiedad horizontal y vertical. Es, también, un movimiento fácil de observar, siendo frecuente en deportes practicados con balones y pelotas.
Ejemplos del movimiento de tiro horizontal
Una persona en patineta, que se desplaza a cierta altura sobre una pista paralela al piso, se puede proyectar horizontalmente y así realizar un salto o una pirueta. Lo mismo puede hacer un esquiador que inicia su salto desde una rampa horizontal, a cierta altura del suelo.
También, es un tiro horizontal el movimiento de un paquete que se suelta desde un avión que vuela horizontalmente, pues el paquete es proyectado con la misma velocidad que lleva el avión.
Ahora, supóngase que un niño, parado a cierta altura sobre el piso, proyecta una bolita de papel con su mano, horizontalmente y hacia adelante. La bolita se convierte entonces en un proyectil.
El tiro horizontal comienza justo en el momento en que se suelta la bolita luego de proyectarla. Una vez hecho esto, la aceleración horizontal del proyectil es 0, mientras que la aceleración vertical es la de la gravedad, dirigida verticalmente y hacia abajo.
De esta manera, la bolita se va moviendo un poco hacia adelante cada vez, al tiempo que cae libremente. El movimiento se descompone en uno horizontal y otro vertical, ambos transcurriendo simultáneamente, pero analizados por separado.
Fórmulas del movimiento explicadas
La siguiente imagen muestra un esquema del tiro horizontal. El proyectil es, en este caso, la pelota que viaja sobre la mesa de altura “h”, con velocidad horizontal de magnitud vo.
Al llegar al borde, la pelota queda librada a la acción de la gravedad. No se toma en cuenta la resistencia que ofrece el aire, pues se considera pequeña, pero esta aproximación generalmente da muy buenos resultados.
Así, el proyectil viaja horizontalmente con movimiento rectilíneo uniforme (sin aceleración) y verticalmente en caída libre.
Antes de escribir las ecuaciones, es necesario establecer un sistema de coordenadas. El sistema elegido tiene su origen en el punto donde la pelota abandona la mesa, el eje horizontal es el eje “x” y el vertical es el eje “y”. Además, se escoge el sentido positivo hacia la derecha y hacia abajo, respectivamente.
Todo esto se muestra en la siguiente figura:
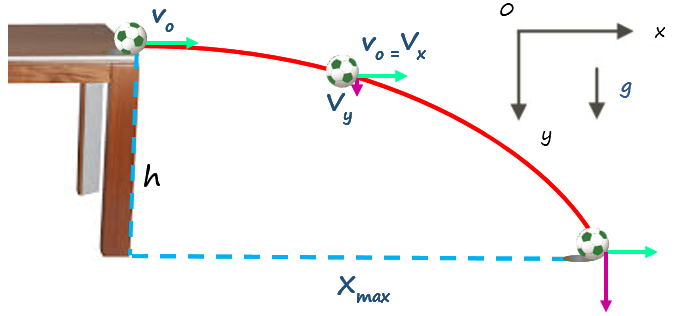
Movimiento horizontal
La ecuación de la posición en función del tiempo “t” para el movimiento horizontal es:
\(x=~{{x}_{o}}+{{v}_{o}}\cdot t\)
Se trata pues, de un movimiento sin aceleración.
Puesto que se escogió la posición inicial xo = 0, la ecuación se reduce a:
\(x={{v}_{o}}\cdot t\)
Movimiento vertical
El movimiento vertical consiste en una caída libre:
\(y=~\frac{1}{2}\cdot g{{t}^{2}}\)
Donde g = 9.8 m/s2 es la magnitud de la aceleración de gravedad.
El tiempo total que el proyectil permanece en el aire depende de la altura desde donde cae:
\(t=\sqrt{\frac{2h}{g}}\)
Y como se puede ver, es el mismo tiempo que tarda si se deja caer libremente desde la altura “h”.
El tiempo se puede despejar de la ecuación para el movimiento horizontal, y luego sustituirse en la del movimiento vertical. De esta manera se obtiene una nueva ecuación, en la que no aparece el tiempo:
\(t=\frac{x}{{{v}_{o}}}\)
\(y=~\frac{1}{2}\cdot g{{\left( \frac{x}{{{v}_{o}}} \right)}^{2}}=\left( \frac{g}{2v_{o}^{2}} \right)\cdot {{x}^{2}}\)
Esta ecuación describe la trayectoria del proyectil, que es una parábola cuya forma es:
\(y=k\cdot {{x}^{2}}\)
donde:
\(k=\frac{g}{2v_{o}^{2}}\).
Por otra parte, el rango o alcance máximo horizontal \({{x}_{max}}\), se obtiene sustituyendo el tiempo de viaje en la ecuación del movimiento horizontal:
\({{x}_{max}}={{v}_{o}}\cdot \left( \sqrt{\frac{2h}{g}} \right)\)
Velocidad en cualquier instante
La velocidad \(\vec{v}~\)es un vector, por lo tanto, tiene componentes horizontal y vertical.
La componente horizontal se mantiene constante en todo momento y es vo. En cambio, la componente vertical varía con el tiempo según \(g\cdot t\) y su magnitud va aumentando a medida que cae.
Por lo tanto, el vector \(\vec{v}~\) queda:
\(\vec{v}=~{{v}_{o~}}\hat{x}+\left( g\cdot t \right)~\hat{y}~\)
La magnitud de la velocidad (la rapidez), se calcula a través de:
\(v=\sqrt{v_{x}^{2}+v_{y}^{2}}=\sqrt{v_{o}^{2}+{{\left( g\cdot t \right)}^{2}}}\)
Ejercicio práctico
La altura de la mesa mostrada en la figura es 1.3 m y la pelota cae más adelante, a 2.1 m del pie de la mesa. ¿Cuánto tiempo demora la pelota en el aire? ¿Qué rapidez tiene al tocar el piso?
Respuestas
El tiempo que tarda en caer es:
\(t=\sqrt{\frac{2h}{g}}=\sqrt{\frac{2\times 1.30m}{9.8~m/{{s}^{2}}}}=0.515~s\)
Para hallar la rapidez se utiliza:
\(v=\sqrt{v_{x}^{2}+v_{y}^{2}}=\sqrt{v_{o}^{2}+{{\left( g\cdot t \right)}^{2}}}\)
Pero antes hay que conocer vo, a partir de:
\(x={{v}_{o}}\cdot t\)
\({{v}_{o}}=\frac{2.1~m}{0.515~s}=4.08~m/s\)
Sustituyendo en la fórmula de la rapidez, queda:
