La elipse es una curva cerrada que pertenece a la familia de las cónicas, compuesta además por la circunferencia, y la parábola. Estas curvas se llaman cónicas, puesto que se obtienen al cortar un cono circular recto con un plano. En particular, la elipse se obtiene al seccionar el cono con un plano cuyo vector normal forma un cierto ángulo respecto al eje del cono.

Desde el punto de vista matemático, la elipse se define como el conjunto de puntos que cumplen la condición de que la suma de sus distancias a los focos, es constante.
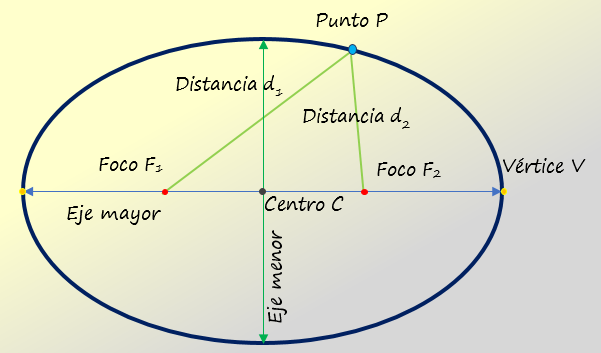
En la figura siguiente se muestran los elementos principales de la elipse, cuya forma está determinada por la longitud de los ejes, uno mayor y otro menor. Los focos son dos puntos ubicados siempre sobre el eje mayor, a ambos lados del centro, que corresponde a la mitad de dicho eje mayor. Los dos vértices son los extremos de este eje, y el eje menor es perpendicular al eje mayor.
Con esto, la definición matemática de la elipse queda simplemente:
\({{d}_{1}}+{{d}_{2}}=constante\)
Donde d1 y d2 son las distancias entre un punto P arbitrario, sobre la elipse, y los respectivos focos de esta.
La elipse es una interesante curva con importante presencia en la naturaleza, nada menos que en el movimiento de la Tierra y los demás planetas alrededor del Sol. En su movimiento de traslación, la Tierra describe una elipse con el Sol en uno de los focos y, asimismo, algunos cometas también tienen trayectorias elípticas.
Ecuaciones canónica y general
Hay varias maneras de expresar matemáticamente una elipse. Están la ecuación canónica y la ecuación general. Comenzando por la ecuación canónica, se distinguen dos casos, el primero es el de la elipse centrada en el origen, y el segundo, cuando el centro tiene coordenadas (h, k). En cuanto a la ecuación general, esta se obtiene desarrollando la ecuación canónica.
Caso 1 en la ecuación canónica: Elipse centrada en el origen
La ecuación para la elipse cuyo eje mayor es horizontal, y con centro en el origen (0,0) de un sistema de coordenadas cartesianas es:
\(\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1\)
Donde “a” es la longitud del semieje mayor y “b” es la longitud del semieje menor. Por lo tanto, el eje mayor mide 2a y el menor 2b.
Por su parte, los focos están equidistantes del centro, separados una distancia llamada “distancia focal”. A la distancia entre el centro y uno de los focos, se la llama “c”, por lo que la distancia focal es 2c.
Existe una relación entre los valores de a, b y c, dada por:
\({{c}^{2}}={{a}^{2}}-{{b}^{2}}\)
Desde luego, se puede tener una elipse cuyo eje mayor sea vertical y esté centrada en (0,0), en cuyo caso, la ecuación correspondiente es:
\(\frac{{{{x}^{2}}}}{{{{b}^{2}}}}+\frac{{{{y}^{2}}}}{{{{a}^{2}}}}=1\)
Como siempre, los focos se ubican sobre el eje mayor de la elipse, ya sea este horizontal o vertical.
Otro detalle importante sobre la elipse es su excentricidad, la cual indica que tan ovalada es. La excentricidad se denota con la letra “e” y es el cociente entre c y a:
\(e=\frac{c}{a}\)
Al ser “a” mayor que “c”, la excentricidad está comprendida entre 0 y 1. Una elipse con excentricidad muy pequeña es casi circular, mientras que otra con excentricidad cercana a 1 es bastante aplanada.
Caso 2 en la ecuación canónica: Elipse con centro en (h, k)
Cuando el centro de la elipse se encuentra en el punto de coordenadas (h, k), las ecuaciones anteriores se transforman en:
\(\frac{{{{{\left( {x-h} \right)}}^{2}}}}{{{{a}^{2}}}}+\frac{{{{{\left( {y-k} \right)}}^{2}}}}{{{{b}^{2}}}}=1\)
Y
\(\frac{{{{{\left( {x-h} \right)}}^{2}}}}{{{{b}^{2}}}}+\frac{{{{{\left( {y-k} \right)}}^{2}}}}{{{{a}^{2}}}}=1\)
Ecuación general de la elipse
Tras desarrollar los cuadrados en la ecuación canónica, la ecuación de la elipse toma la forma:
\(A{{x}^{2}}+B{{y}^{2}}+Cx+Dy+E=0\)
Cuyas particularidades son las siguientes:
A > 0, B > 0, A ≠ B
Es decir, los coeficientes A y B siempre son positivos, y A es distinto de B.
Ejercicio paso a paso
Hallar la ecuación de la elipse centrada en el origen, cuyos vértices están en los puntos (−7,0) y (7,0), sabiendo que su excentricidad es e = 4/7.
Respuesta
Como la elipse está centrada en el origen, los vértices equidistan del punto (0,0), 7 unidades a la izquierda y 7 a la derecha, por lo tanto, a = 7. El eje mayor de la elipse está sobre el eje horizontal, como se advierte observando que la coordenada “y” de los vértices es nula.
A partir de la ecuación para la excentricidad:
\(e=\frac{c}{a}\)
Y sabiendo que:
\({{c}^{2}}={{a}^{2}}-{{b}^{2}}\)
Se sustituye en la expresión de la excentricidad:
\(e=\frac{{\sqrt{{{{a}^{2}}-{{b}^{2}}}}}}{a}\)
Elevando al cuadrado en ambos lados, para eliminar la raíz:
\({{e}^{2}}=\frac{{{{a}^{2}}-{{b}^{2}}}}{{{{a}^{2}}}}\)
Ahora se despeja el valor de “b”, que es la longitud del semieje menor:
\({{b}^{2}}={{a}^{2}}-{{e}^{2}}\cdot {{a}^{2}}\)
Por lo tanto:
\(b=\sqrt{{{{a}^{2}}-{{e}^{2}}\cdot {{a}^{2}}}}=\sqrt{{{{7}^{2}}-{{{\left( {\frac{4}{7}} \right)}}^{2}}{{{\cdot 7}}^{2}}}}=\sqrt{{33}}\)
La ecuación de la elipse es:
\(\frac{{{{x}^{2}}}}{{{{7}^{2}}}}+\frac{{{{y}^{2}}}}{{{{{\left( {\sqrt{{33}}} \right)}}^{2}}}}=1\)
\(\frac{{{{x}^{2}}}}{{49}}+\frac{{{{y}^{2}}}}{{33}}=1\)
Referencias bibliográficas
- Hoffman, J. Selección de Temas de Matemática. Vol. 5. Editorial Sphinx.- Swokowski, E. 2011. Álgebra con Trigonometría y Geometría Analítica. 13va. Edición. Cengage Learning.
