Definición de Principio de Incertidumbre desarrollo histórico, y fórmulas

El Principio de Incertidumbre, a veces también referido como Principio de Indeterminación, es uno de los principales pilares de la Mecánica Cuántica. El principio de incertidumbre establece que es imposible medir simultáneamente dos magnitudes conjugadas con un nivel de precisión absoluto. Dicho con otras palabras, reducir la incertidumbre en la medición de una cantidad intrínsecamente aumenta la incertidumbre en la medida de su magnitud conjugada.

La Mecánica Cuántica es una rama de la Física que sostiene a gran parte de la Física Moderna. A su vez, es la teoría física más precisa que tenemos hasta al momento, pero también la más contraintuitiva que existe. El principio de incertidumbre es una de las manifestaciones más fascinante que tiene la mecánica cuántica en el mundo subatómico.

Desarrollo histórico

El viaje a través del mundo cuántico comenzó recién entrado el Siglo XX, cuando Max Planck explicó la radiación del cuerpo negro asumiendo que la energía estaba discretizada en pequeños paquetes a la cuales llamó “cuantos”, de aquí es que viene la palabra “cuántica”.

Años más tarde, en 1905, Albert Einstein utilizó esta hipótesis de Planck para explicar el efecto fotoeléctrico, lo cual le valió el Premio Nobel de Física en 1921. En 1913 Niels Bohr también utilizó la hipótesis de Planck para explicar cómo los electrones se distribuyen en niveles específicos de energía alrededor del núcleo atómico, resolviendo así el problema que planteaba el modelo atómico de Rutherford.

La hipótesis de Planck y los trabajos de Einstein y Bohr implicaban que la luz se podía comportar como partícula. Sin embargo, esto contradecía a la teoría electromagnética y a resultados experimentales que habían demostrado que la luz era una onda electromagnética, y ponía de nuevo sobre la mesa este dilema sobre la naturaleza de la luz.

En 1924 Louis de Broglie propuso de hipótesis ondulatoria de la materia con el objetivo de explicar esta naturaleza dual que parecía tener la luz. No obstante, esto implicaba que también las partículas podían comportarse como ondas. Basándose en esta hipótesis fue que en 1926 Erwin Schrödinger formuló su famosa ecuación que describe la evolución temporal de las partículas subatómicas en función de sus propiedades ondulatorias.

Clinton Davisson y Lester Germer en 1927 demostraron experimentalmente que las partículas tenían este comportamiento ondulatorio descrito por de Broglie y Schrödinger, este es el famoso experimento de la doble rendija. Ya no quedaba duda alguna de que las partículas tenían propiedades ondulatorias y después de esto se comenzó a indagar en las implicaciones que esto tenía.

En el año 1927 Werner Heisenberg se dio cuenta que una implicación de esta naturaleza ondulatoria de la materia es que no se puede conocer con exactitud la posición de la partícula y su momento lineal simultáneamente. Medir con gran precisión una de estas magnitudes provoca que se tenga mayor incertidumbre sobre la otra magnitud. Esto es el Principio de Incertidumbre, muchas veces también conocido como “Principio de Incertidumbre de Heisenberg” en honor a Werner Heisenberg.

Fórmulas

El principio de incertidumbre de Heisenberg matemáticamente se expresa como:

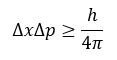
Donde Δx representa la incertidumbre sobre la posición, Δp es la incertidumbre sobre el momento lineal y h es la constante de Planck. El valor de esta constante es: h≈6.626×10^(-34) J/s. Muchas veces en mecánica cuántica se utiliza la constante de Planck reducida, la cual se define como:

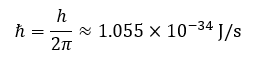
Esto nos permite reescribir el principio de indeterminación de Heisenberg como:

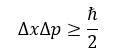
Como podemos darnos cuenta, el principio de incertidumbre es una inecuación, esto quiere decir que fijando el valor de una de las variables hace que la variable restante pueda tomar un rango de valores para satisfacer la inecuación.

Por ejemplo, supongamos que logramos medir con gran precisión la posición de una partícula, esto quiere decir que la incertidumbre sobre su posición Δx es muy pequeña. Como la multiplicación entre esta incertidumbre y la incertidumbre del momento lineal Δp debe ser mayor o igual a ℏ/2, entonces Δp debe tener un valor más grande y encontrarse en un rango más amplio para satisfacer esto. Esto es precisamente lo que establece el principio de incertidumbre.

En este caso hemos formulado el principio de incertidumbre para la posición y el momento lineal, y generalmente es el caso que se presenta cuando se estudia este tema, sin embargo, el principio de incertidumbre aplica para cualquier par de magnitudes físicas conjugadas o que se encuentren relacionadas. Otro ejemplo es la indeterminación existente entre la energía E y el tiempo t, esto se expresa como:

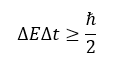
La implicación del principio de incertidumbre en estas dos cantidades es la existencia de partículas virtuales que se generan y desintegran constantemente en el vacío cuántico.

Cabe destacar que debido a que la constante de Planck tiene un valor tan pequeño, el principio de incertidumbre sólo se manifiesta en el mundo subatómico. A escalas macroscópicas los efectos de principio de incertidumbre prácticamente son despreciables y por ello podemos conocer simultáneamente y con precisión el valor de pares de magnitudes conjugadas.