La precesión es el movimiento giratorio que experimenta el eje de un objeto en rotación, y como consecuencia, el eje describe un cono. El ejemplo más familiar es el de un trompo o peonza que gira, en el cual se observa que el eje de rotación barre un cono imaginario, cuya punta coincide con el punto de apoyo.
Una peonza que no está dando vueltas, cae sin remedio al suelo, porque su centro de masas CM deja de estar alineado con el punto de apoyo. Entonces su peso, aplicado al CM, ejerce un torque respecto a dicho punto de apoyo, haciendo que el trompo se vuelque.
La Tierra también experimenta un movimiento de precesión, aparte de la traslación anual alrededor del Sol y la rotación alrededor de su propio eje. Se conoce como la precesión de los equinoccios.
Ocurre que el eje de rotación terrestre tiene una inclinación de 23.5º respecto a la perpendicular del plano de su órbita (el plano de la eclíptica) y, además, no es una esfera perfecta. Por lo tanto, precesa en torno a dicha perpendicular, debido a los torques que generan las fuerzas gravitacionales ejercidas por el Sol y la Luna.
El período de precesión de la Tierra es de unos 26.000 años, por lo que no es tan perceptible como los movimientos principales de rotación y traslación. Sin embargo, a la larga, la precesión hará que Polaris, la estrella que actualmente señala la ubicación del polo norte, deje de hacerlo dentro de algunos miles de años.
De hecho, los astrónomos han determinado que hace 5000 años la estrella polar era Alfa Draconis, y que la próxima estrella polar será Alfa Cefeida, a 68º de Polaris, ubicada sobre el círculo que describe el eje terrestre durante su precesión. De manera que lenta, pero inexorablemente, la posición de las constelaciones irá cambiando con el tiempo, debido a la precesión terrestre.
Ejemplos
La precesión del trompo
Se puede explicar el origen de la precesión tomando como ejemplo el movimiento del trompo o peonza. Hay dos fuerzas sobre el punto de apoyo: la normal, aplicada perpendicularmente en la punta del trompo y dirigida hacia arriba, y el peso aplicado en el centro de masas del trompo y apuntando verticalmente hacia abajo.
Respecto al punto de apoyo, la normal no ejerce momento de torsión o torque, pero el peso sí lo hace, cuando el eje de rotación no es perpendicular al suelo. Todo esto se ilustra en la figura a), mostrada a continuación:
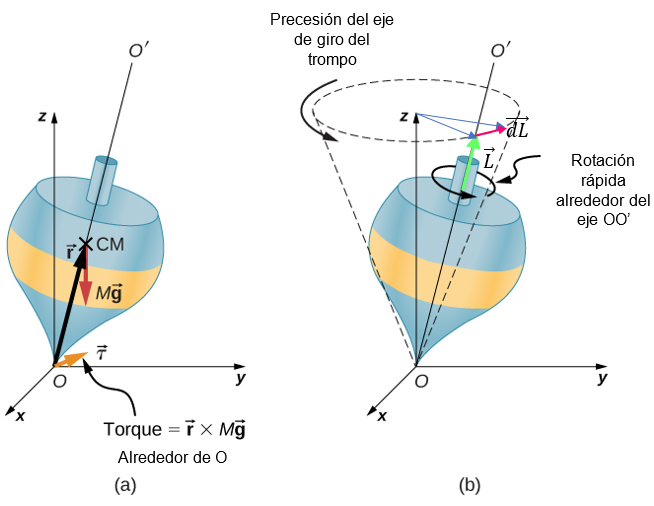
Figura basada en el trabajo de University Physics, Vol. 1, de la Universidad de Rice.
Una peonza que no gira
Es sabido que, si la peonza no está rotando sobre su eje, invariablemente se desploma. Esto se debe al torque respecto al punto de apoyo, producido por el peso. Dicho torque es el producto vectorial entre los vectores \(\vec{r}\) y \(M\vec{g}\), y es perpendicular al plano conformado por \(\vec{r}\) y \(M\vec{g}\):
\(\vec{\tau }=\vec{r}\times M\vec{g}\)
Por ejemplo, si ambos vectores están en el plano zy, el torque se dirige a lo largo del eje x, y en el caso mostrado en la figura, entrando a la pantalla. Así, la peonza rota alrededor de x en sentido horario, lo cual significa que termina por caer.
La peonza en rotación
Pero, si la peonza se lanza para hacerla rotar en posición vertical sobre una superficie muy lisa, se mantendrá en esa posición, porque así la línea de acción del peso pasa por el eje de rotación y, por lo tanto, su torque es nulo, según se explicó antes.
Ahora bien, como cualquier objeto que rota, la peonza posee momento angular \(\vec{L}\), un vector dirigido a lo largo del eje de rotación. Cuando este eje se mantiene vertical, \(\vec{L}\) es constante y el trompo gira indefinidamente con velocidad angular uniforme.
Sin embargo, si existe algo de rozamiento en el punto de apoyo, el eje se inclina, formando un ángulo con la vertical, y entonces el peso ejerce su torque, haciendo que la dirección del momento angular deje de ser constante.
La variación en el momento angular equivale al torque aplicado:
\(\vec{\tau }=\frac{{d\vec{L}}}{{dt}}\)
La ecuación anterior puede ser escrita en forma diferencial de la siguiente manera:
\(\text{d}\vec{L}=\vec{\tau }\text{d}t\)
Esta ecuación se interpreta así: en un lapso de tiempo infinitesimal \(\text{d}t\), el cambio en el momento angular \(d\vec{L}\) es paralelo al torque \(\vec{\tau }\).
Puesto que el torque es perpendicular al momento angular y paralelo al plano horizontal (ver figura b), solamente ocasiona cambios en la dirección de \(\vec{L}\), pero manteniendo constante su módulo. Es análogo al efecto de la aceleración centrípeta en el movimiento circular uniforme, la cual, siendo perpendicular a la velocidad, hace que esta cambie de dirección, describiendo una circunferencia, pero manteniendo constante su módulo.
