La pirámide es una figura tridimensional formada por una base poligonal, de la cual parten segmentos que se reúnen en un solo punto, ubicado a cierta altura de dicha base, delimitando así las caras laterales de la pirámide, cuya forma es triangular.
Cualquier polígono puede servir como base, por lo que pueden construirse pirámides con base triangular, cuadrada, pentagonal y más. El número de caras laterales de la pirámide es igual al número de lados de la base. Por ejemplo, si esta es un triángulo, entonces la pirámide tiene 3 caras laterales, si es un cuadrado, entonces habrá 4 caras laterales, y así sucesivamente.
La forma piramidal ha fascinado desde antaño a la humanidad, lo cual se evidencia en numerosas construcciones dejadas por antiguas culturas del Viejo y el Nuevo Mundo. Destacan los zigurats de Mesopotamia, las pirámides mayas y aztecas, pero las más emblemáticas son, sin duda alguna, las pirámides del antiguo Egipto, construidas como monumentos funerarios a los faraones.
Las pirámides también forman parte de algunos edificios más recientes, rematando torres o campanarios, o bien como elemento decorativo, en el caso de la pirámide del museo del Louvre en París o los billetes de un dólar.
Tipos de pirámides
Las pirámides se clasifican de acuerdo a la forma de sus caras laterales, según los siguientes criterios:
• Rectas, si sus caras laterales son triángulos isósceles.
• Oblicuas, si alguna de las caras laterales no es un triángulo isósceles
Otro criterio hace referencia al polígono que hace de base. De acuerdo a ello se tienen pirámides:
• Regulares, si la base es un polígono regular y la pirámide es recta. En tal caso, las caras laterales son idénticas.
• Irregulares, cuando la base es un polígono irregular, o si alguna de sus caras es un triángulo no isósceles, es decir, se trata de una pirámide oblicua.
• Triangulares, cuadrangulares, pentagonales y más, de acuerdo al número de lados de la base.
• Cóncavas, si la base es un polígono cóncavo (alguno de sus ángulos internos es mayor a 180º).
• Convexas, cuando todos los ángulos internos de la base piramidal son menores que 180º.
Elementos de la pirámide
Una pirámide está caracterizada por los siguientes elementos:
1. Base, el elemento distintivo, puede ser cualquier polígono, sin importar si es o no regular, y puede tener cualquier número de lados.
2. Caras laterales, siempre son triángulos.
3. Ápice o vértice principal, es el punto ubicado por encima de la base, en el que se juntan los vértices de las caras laterales.
4. Altura, distancia entre la base y el ápice.
5. Altura inclinada, también llamada apotema de la pirámide, es el segmento que conecta el ápice con un lado de la base, equivalente a la altura del triángulo que hace de cara lateral. Esta apotema solo existe en pirámides regulares.
6. Apotema de la base, línea que une a un lado de la base con su centro geométrico, y solo existe cuando la pirámide es regular.
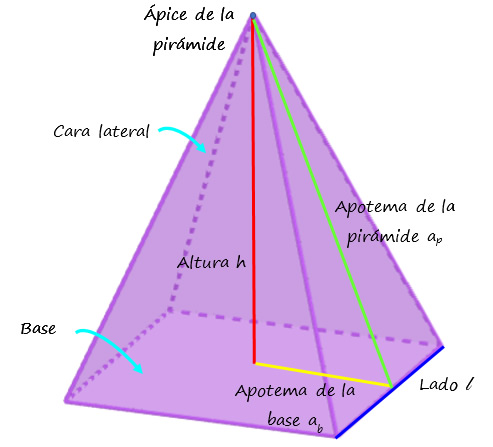
Estos elementos participan en las fórmulas que permiten calcular el área superficial y el volumen de una pirámide. Por eso es necesario conocer su ubicación, ya que hay muchos tipos de pirámides. Se muestran en la siguiente figura, que corresponde a una pirámide cuadrangular, una cuya base es un cuadrilátero.
¿Cómo calcular el área superficial y volumen de una pirámide?
Imaginando que la pirámide se puede desarmar y extender sobre una superficie plana, su área A resulta ser la suma del área de su base y el área de cada una de sus caras laterales:
\(A=\) \({{A}_{{base}}}+~{{A}_{{caras}}}\)
Esta expresión se aplica a cualquier clase de pirámide, ahora bien, cuando la pirámide es regular, el área superficial se puede calcular conociendo el valor de las apotemas.
Sea una pirámide cuya base es el polígono de N lados, su área superficial A es:
\(A=~\left( {\frac{{N\cdot \ell }}{2}} \right)\times \left( {a{{p}_{{base}}}+a{{p}_{{pir\acute{a}mide}}}} \right)\)
Donde:
• La base es \(\ell \)
• \(a{{p}_{{base}}}\) denota la apotema de la base
• \(a{{p}_{{pir\acute{a}mide~}}}\) es la apotema de la pirámide
En la figura anterior, los segmentos rojo, verde y amarillo son los lados de un triángulo rectángulo. Por lo tanto, las apotemas y la altura de una pirámide regular, están relacionadas a través del teorema de Pitágoras, como sigue:
\(ap_{{p~}}^{2}=~ap_{b}^{2}+~{{h}^{2}}\)
Para el volumen de la pirámide también hay una fórmula general, válida para cualquier pirámide, que es la siguiente:
\(V=\frac{1}{3}\cdot {{A}_{{base}}}\cdot h\)
A su vez, el área de la base dependerá de la forma que esta tenga. Por ejemplo, si la base de la pirámide es cuadrada de lado “a”, el volumen será:
\(V=\frac{1}{3}\cdot {{a}^{2}}\cdot h\)
