El campo eléctrico (\(\vec{E}\)) puede representarse a través de líneas imaginarias denominadas líneas de campo eléctrico. La definición de flujo eléctrico (ΦE) se encuentra asociada a estas líneas de campo. Cuando estas líneas de campo atraviesan una superficie, es decir, entran o salen de la misma, se dice que existe un flujo eléctrico a través de la superficie. El número neto de líneas que atraviesan a la superficie es proporcional a la carga neta dentro de dicha superficie.
Ejemplos ilustrativos
Para entender mejor el concepto de flujo eléctrico se utilizará en siguiente ejemplo mostrado en la figura, donde se presentan unas cajas dentro de las cuales se ubican diferentes cargas puntuales y se dibujan las líneas de campo eléctrico correspondientes a cada tipo de carga.
A continuación, se describe el flujo eléctrico en cada una de las cinco cajas mostradas en la figura anterior, en función de la carga neta que encierran y del comportamiento de las líneas de campo eléctrico:
• Figura a): la caja encierra una carga positiva y las líneas de campo salen de la misma, por lo tanto, el flujo eléctrico a través de la superficie será positivo (\(ΦE > 0\))
• Figura b): existe una carga negativa dentro de la caja, las líneas de campo entran en la superficie, por lo tanto, el flujo eléctrico a través de la misma será negativo (\(ΦE < 0\)).
• Figura c): la caja no está encerrando ninguna carga (ninguna línea de campo la atraviesa) y el flujo a través de ella es cero (\(ΦE = 0\)).
• Figura d): la caja está encerrando a un dipolo eléctrico, por lo que la carga neta encerrada es cero, y el número de líneas de campo que entran es igual al número de líneas de campo que salen, es decir, el número neto de líneas es cero, por lo tanto, la superficie tiene un flujo eléctrico igual a cero (\(ΦE = 0\)).
• Figura e): la caja no está encerrando ninguna carga, las líneas de campo eléctrico son generadas por alguna carga ubicada fuera de la misma (el mismo número de líneas entran y salen de la superficie) por lo tanto no existe flujo eléctrico a través de la superficie (\(ΦE = 0\)).
Si la caja mostrada en la figura la sustituyéramos por una caja más grande o más pequeña, o inclusive la cambiásemos por alguna otra superficie cerrada, el número de líneas que atravesarían la superficie continuaría siendo el mismo, y el flujo eléctrico a través de la superficie de las figuras a), b), c), d) y e) continuaría siendo el mismo que se indicó en la descripción anterior.
A partir de lo explicado anteriormente, se puede concluir lo siguiente:
1) El que exista flujo eléctrico neto hacia adentro o hacia afuera de la superficie dependerá del signo de la carga neta encerrada.
2) Las cargas que se encuentran fuera de la superficie no generan flujo eléctrico neto a través de dicha superficie.
3) El flujo eléctrico neto es directamente proporcional a la carga eléctrica neta encerrada en la superficie e independiente de la forma o tamaño de dicha superficie.
Fórmulas para calcular el flujo eléctrico
Para calcular el flujo eléctrico se utilizará inicialmente una superficie abierta y un campo eléctrico uniforme. Supongamos que tenemos un área o superficie plana, como por ejemplo un rectángulo, y un campo eléctrico uniforme, como se muestra en la figura.
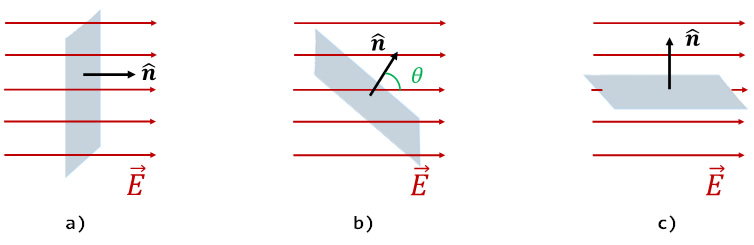
En la figura a) la superficie es perpendicular a la dirección del campo eléctrico y todas las líneas del campo eléctrico están atravesando a dicha área. Si giramos la superficie con respecto a la dirección del campo eléctrico, como se muestra en la figura b), el número de líneas que atraviesa la superficie es menor, y si la superficie está paralela a la dirección del campo eléctrico como se muestra en la figura c), ninguna línea de campo la atravesará.
Como se pudo apreciar en la figura anterior, el número de líneas que atraviesa a la superficie depende de la orientación de ésta con respecto a las líneas de campo eléctrico, por lo tanto, el flujo eléctrico a través de dicha superficie debe ser definido de forma tal que tome en cuenta este hecho.
Se define al flujo eléctrico (ΦE) como una cantidad escalar igual al producto escalar entre el vector campo eléctrico y el vector área, es decir,
\({{\text{ }\!\!\Phi\!\!\text{ }}_{\text{E}}}\text{ }\!\!~\!\!\text{ }=\text{ }\!\!~\!\!\text{ }\vec{E}\cdot \vec{A}=EA\cos \theta ~~~~~;~~~~0{}^\circ ~\le ~\theta ~\le 180{}^\circ \)
Donde el vector área se define como: \(\vec{A}=A~\hat{n}\), siendo \(\hat{n}\) un vector unitario perpendicular a la superficie y \(A\) la magnitud del área de dicha superficie. Cuando se calcula el flujo eléctrico a través de una superficie cerrada, el vector \(\hat{n}\) siempre es perpendicular a la superficie y saliendo de ésta, para el caso de superficies abiertas se debe especificar la dirección elegida.
La unidad del flujo eléctrico es \(N\cdot {{m}^{2}}/C\).
Cuando el campo eléctrico es perpendicular a la superficie (\(\theta =0{}^\circ \)), como en la figura a), el flujo eléctrico es máximo e igual al producto de \(EA\); si la superficie es paralela al campo (\(\theta =90{}^\circ \)), como en la figura c), el flujo eléctrico es nulo; mientras que si la superficie y el campo eléctrico forman cualquier otro ángulo \(\theta \) entre ellos, el flujo eléctrico será igual a \(EA\cos \theta \) .
Si el campo eléctrico \(\vec{E}~\) no es uniforme o si la superficie es curva, para calcular el flujo eléctrico a través de la misma, ésta se divide en muchas áreas, tan pequeñas que pueden ser consideradas como planas, cada una con un área igual a \(dA\), un vector \(\hat{n}\) perpendicular a la misma y un \(\overrightarrow{dA}=dA~\hat{n}\) , donde el campo eléctrico puede ser considerado como uniforme.
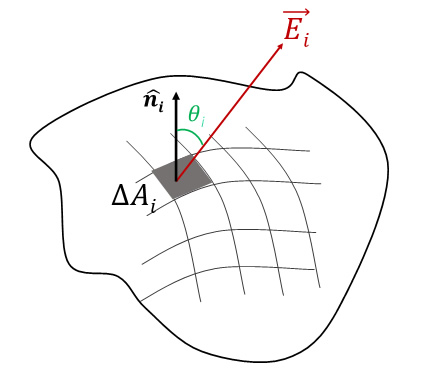
El flujo eléctrico total sobre la superficie será igual a la suma de las contribuciones del flujo que realiza cada una de las áreas infinitesimales. Si el número de elementos de área tiende a infinito y se aplica el límite, la sumatoria se convierte en una integral de superficie.
Generalmente se está interesado en calcular el flujo eléctrico a través de una superficie cerrada. Se define una superficie cerrada como aquella que divide el espacio en un una región interior y una región exterior, de forma tal que no es posible moverse de una región a la otra sin atravesar o cruzar a la superficie. El flujo eléctrico para una superficie cerrada está dado por:
ΦEt = ∯s E ⃗ ∙ dA ⃗ = ∯s E ⃗ ∙ dA n ̂
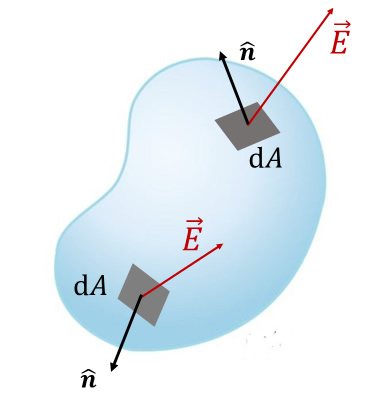
El flujo eléctrico total a través de la superficie cerrada puede ser positivo, negativo o cero. Si ΦEt = ∯s E ⃗ ∙ dA ⃗ > 0, las líneas de campo eléctrico salen de la superficie, mientras que si ΦEt = ∯s E ⃗ ∙ dA ⃗ < 0, las líneas de campo eléctrico entran a la superficie.
Autora
Escrito por Lismarihen Larreal para la Edición #105 de Enciclopedia Asigna, en 11/2021. Lismarihen es Ingeniera Mecánica, con maestría en Física Aplicada y doctorado en Ingeniería Ambiental, asímismo se desempeña como Docente e Investigadora en el Depto. de Física de la Facultad de Ingeniería de la Universidad del Zulia.