El dipolo eléctrico es una configuración de dos cargas eléctricas puntuales de igual magnitud, pero de signo contrario (\(+q~,~-q)\) separadas una distancia d. Matemáticamente, se caracteriza por tener asociado un momento dipolar eléctrico (\(\vec{\rho }\)), que se define como el producto entre la magnitud de la carga eléctrica del dipolo multiplicada por la distancia de separación entre ellas.
El momento dipolar eléctrico es un vector cuya dirección y sentido siempre es de la carga negativa hacia la positiva, como se muestra en la figura 1. Se expresa en Coulomb por metro (\(C \cdot m\)).
\(\rho =q \cdot d\)
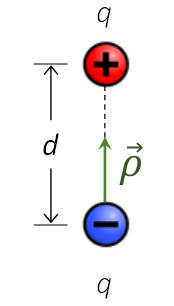
Figura 1. Dipolo eléctrico y momento dipolar eléctrico.
Diferencia entre dieléctricos con moléculas polares y no polares
Un dipolo eléctrico aparece en los materiales dieléctricos, también conocidos como materiales aislantes, en los cuales no hay electrones libres. Los materiales dieléctricos pueden estar constituidos por moléculas polares o moléculas no polares.
En los dieléctricos con moléculas polares, los centros de distribución de las cargas positivas y negativas no coinciden, por lo tanto, este tipo de materiales poseen momento dipolar eléctrico permanente, el cual se encuentra orientado de forma aleatoria en su interior. Un ejemplo de este tipo de moléculas es la molécula de agua, donde los iones hidrógeno no están alineados con el ion oxígeno, sino que se encuentran en una disposición triangular como se muestra en la figura 2.
Por el contrario, en los dieléctricos constituidos por moléculas no polares, los centros de distribución de las cargas positivas y negativas coinciden, por lo tanto, carecen de momento dipolar permanente, sin embargo, pueden adquirirlo por inducción. Un ejemplo de este tipo de moléculas seria en oxígeno (\({{O}_{2}}\)), el nitrógeno (\({{N}_{2}}\)), entre otros, las cuales están constituidas por dos átomos iguales (ver figura 2).
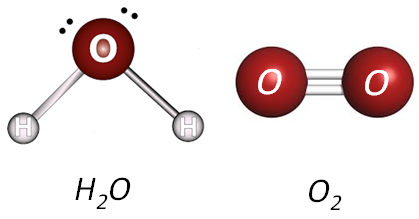
Figura 2. Representación de la molécula de agua (\({{H}_{2}}O\)) y de oxígeno (\({{O}_{2}}\)).
Polarización
Cuando un material dieléctrico es sometido a la influencia de un campo eléctrico externo, se produce en el interior del material un reordenamiento de la carga a nivel microscópico que genera la aparición de los dipolos eléctricos, los cuales tienden a orientarse en la dirección del campo eléctrico externo aplicado. A esta orientación de los dipolos eléctricos dentro del material, se le conoce como polarización.
Esta polarización que sufre el material dieléctrico, produce un debilitamiento del campo eléctrico en el interior del material, ya que la alineación interna de los dipolos eléctricos produce un campo eléctrico interno en dirección contraria al aplicado.
Efecto de un campo eléctrico uniforme sobre un dipolo eléctrico
Considere el dipolo eléctrico mostrado en la figura 3, el cual se encuentra sometido a la acción de un campo eléctrico uniforme \(\vec{E}\) .
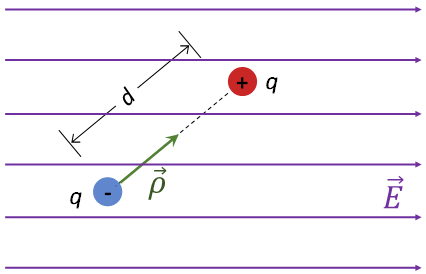
Figura 3. Dipolo eléctrico en presencia de un campo eléctrico uniforme \(\vec{E}\) .
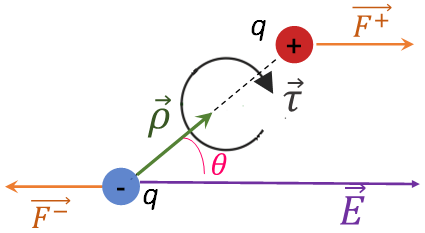
En presencia del \(\vec{E}\) las cargas que constituyen al dipolo experimentan una fuerza eléctrica, cuya magnitud está dado por \(F=qE\). La fuerza eléctrica sobre la carga positiva (\(\overrightarrow{{{F}^{+}}}\)) del dipolo estará en la misma dirección y sentido que el \(\vec{E}\) , mientras que la fuerza eléctrica sobre la carga negativa (\(\overrightarrow{{{F}^{-}}}\)) estará en la misma dirección, pero sentido contrario al \(\vec{E}\), tal como se indica en la figura 4. Donde:
\(\overrightarrow{{{F}^{+}}}=~-\overrightarrow{{{F}^{-}}}\)
\(\left| \overrightarrow{{{F}^{+}}} \right|=~\left| \overrightarrow{{{F}^{-}}} \right|=qE\)
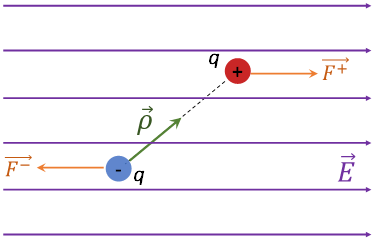
Figura 4. DCL de las fuerzas que actúan sobre un dipolo eléctrico en presencia de un \(\vec{E}\).
Al observar la figura anterior, se aprecia que ambas fuerzas constituyen lo que se conoce como un par de fuerzas (sistema formado por dos fuerzas de igual magnitud, sentido contrario y no colineales). El efecto que produce este par de fuerzas sobre el sistema es de rotación (momento de torsión), tendiendo a alinear al momento dipolar con el campo eléctrico.
El momento de torsión del par de fuerzas es:
\(\vec{\tau }=~\vec{\rho }~\times ~\vec{E}~~~~~\left( N \cdot m \right)\)
\(\tau =~\rho ~E~sen\theta ~~~~;~~~~0~\le ~\theta ~\le 180{}^\circ \)
Donde \(\theta \) representa el ángulo entre \(\vec{\rho }\) y \(\vec{E}\).
El sistema experimentará un momento de torsión máximo cuando \(\vec{\rho }\) Ʇ \(\vec{E}\) (\(\theta =~90\)). La posición de \(\theta =~0\) se conoce como la posición de equilibrio estable, mientras que la posición de \(\theta =~180\) es la posición de equilibrio inestable (el momento de torsión siempre tiende a alinear a \(\vec{\rho }\) con \(\vec{E}\)).
Autora
Escrito por Lismarihen Larreal para la Edición #104 de Enciclopedia Asigna, en 10/2021. Lismarihen es Ingeniera Mecánica, con maestría en Física Aplicada y doctorado en Ingeniería Ambiental, asímismo se desempeña como Docente e Investigadora en el Depto. de Física de la Facultad de Ingeniería de la Universidad del Zulia.