El desplazamiento es una cantidad física vectorial que se define como el cambio de posición, básicamente, de un lugar a otro, que manifiesta un cuerpo, y suele confundirse con la distancia. Desde el punto de vista físico y matemático, la distancia es una cantidad escalar, expresada en unidades de longitud. Físicamente el término distancia se refiere a la magnitud de un desplazamiento, es decir, la longitud entre dos puntos dados; mientras que al hablar de distancia recorrida nos referimos a la longitud total del camino avanzado entre dos puntos dados, es decir, la longitud total de la trayectoria realizada.
Matemáticamente, el desplazamiento se define como un vector que va de la posición inicial hacia la posición final, para lo cual se trabaja la ecuación
\(~\overrightarrow{{{∆x}}}=~\overrightarrow{{{x}_{f}}}-~\overrightarrow{{{x}_{i}}}~\)
Donde \(\overrightarrow{{{x}_{f}}}\) representa la posición final y \(\overrightarrow{{{x}_{i}}}\) la posición inicial. Las unidades del desplazamiento son las mismas unidades de longitud en que se expresa la posición, es decir, metros (m) para el SI.
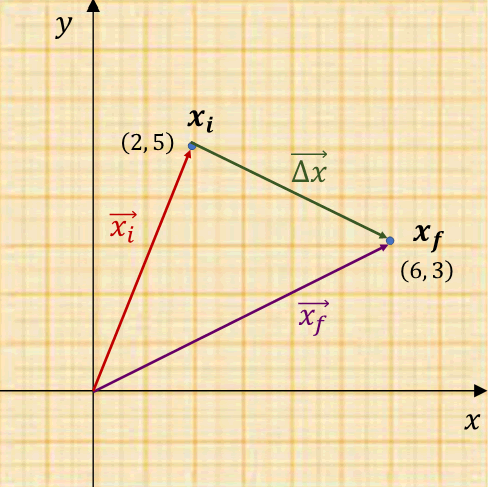
Figura 1. Representación de los vectores posición y desplazamiento. Los puntos inicial y final están ubicados en el plano \(x,~y\).
De acuerdo a lo mostrado en la figura 1, la posición inicial está dada por el vector \(\overrightarrow{{{x}_{i}}}~=2\hat{i}+5\hat{j}\), mientras que la posición final es el vector \(\overrightarrow{{{x}_{f}}}~=6\hat{i}+3\hat{j}\). A partir de estos vectores posición podemos calcular el vector desplazamiento como:
\(~\overrightarrow{{{∆x}}}=~\overrightarrow{{{x}_{f}}}-~\overrightarrow{{{x}_{i}}}=\left( 6\hat{i}+3\hat{j} \right)-(2\hat{i}+5\hat{j}\))
\(~\overrightarrow{{{∆x}}}=~4\hat{i}-2\hat{j}\)
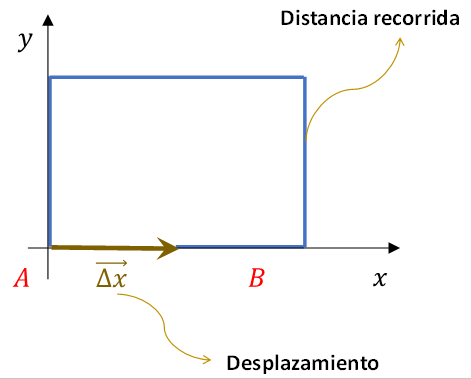
En la figura 2 se representa la distancia recorrida y el desplazamiento, realizado por un cuerpo al moverse desde el punto A hasta el punto B. La línea azul es la trayectoria seguida por el cuerpo al moverse desde su posición inicial (A) hasta su posición final (B), es decir, la distancia recorrida por el cuerpo.
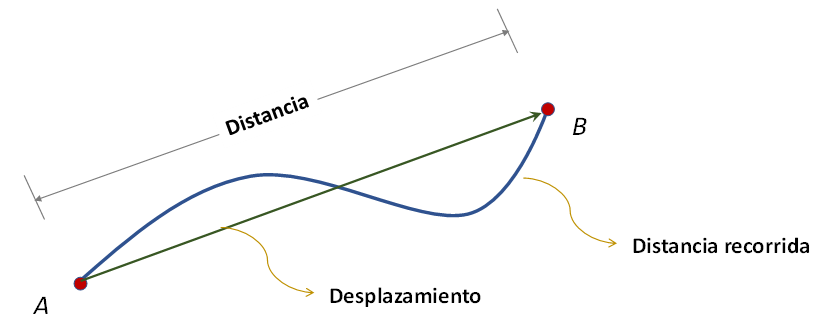
Figura 2. Representación del desplazamiento, distancia y distancia recorrida por un cuerpo que se mueve desde A hasta B.
Ejemplo práctico de la diferencia entre el desplazamiento y la distancia recorrida
Un barco parte del punto A hacia el punto B realizando el siguiente recorrido: 200 metros hacia el norte, 500 metros hacia el este, 200 metros hacia el sur y 300 metros hacia el oeste, como se muestra en la figura. Determine la distancia recorrida y su desplazamiento.
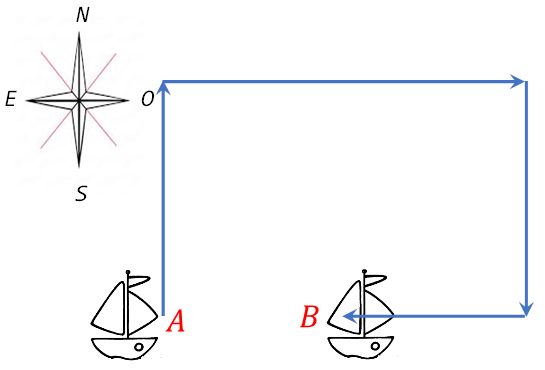
Para determinar la distancia recorrida y el desplazamiento realizado por el barco, debemos dibujar un sistema de referencia y representar el recorrido o trayectoria realizada desde su partida del punto A hasta su llegada al punto B. El origen de nuestro sistema de referencia lo ubicaremos en el punto de partida del barco (A).
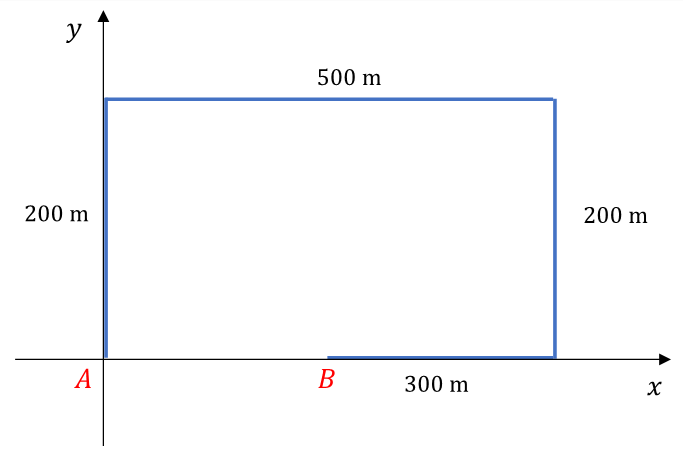
La distancia recorrida por el barco será igual a la suma de cada uno de los recorridos realizados, es decir, 200 + 500 + 200 + 300, así:
\(Distancia~recorrida=1200~m\)
El desplazamiento, por definición, se calcula a partir del vector posición inicial y final. El vector posición inicial y final se determinan a partir de las coordenadas de los puntos A y B, respectivamente.
\(\overrightarrow{{{x}_{i}}}=0\hat{i}+0\hat{j}\)
\(\overrightarrow{{{x}_{f}}}=200\hat{i}+0\hat{j}\)
Por lo tanto, el desplazamiento será:
\(~\overrightarrow{{{∆x}}}=~\overrightarrow{{{x}_{f}}}-~\overrightarrow{{{x}_{i}}}=200~\hat{i}\)
Como se puede apreciar, el barco recorrió 1200 m para moverse desde el punto A al B, pero sólo se desplazó 200 m en dirección hacia el oeste.
Sistema de referencia y Posición
• Sistema de referencia: comprende el conjunto de coordenadas espacio-temporales, donde se representan los puntos y vectores que permiten describir el comportamiento de los cuerpos y partículas. En física se suele utilizar, para estudiar el comportamiento de los cuerpos, el sistema de referencia cartesiano, ya sea, en el plano o en el espacio, donde la ubicación de una partícula o cuerpo se expresa en función de sus coordenadas \(x,~y,z\).
Los sistemas de referencia se pueden ubicar en puntos fijos o móviles e inclusive en el ojo del observador del evento en estudio.
Como ejemplo consideremos el bus y el auto que se muestran en la figura. Para estudiar el movimiento de ambos es preciso ubicar un sistema de referencia. Podemos ubicarlo en el semáforo, en el bus, en el auto o en el perro (observador).
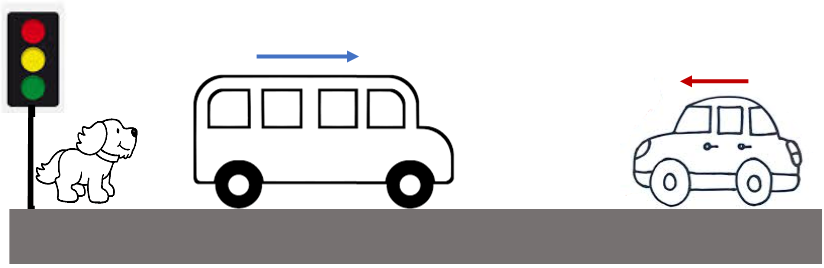
A continuación, estudiaremos el movimiento dependiendo de la ubicación del sistema de referencia:
1. Si ubicamos muestro sistema de referencia en un punto fijo (el semáforo) describiríamos el movimiento de ambos cuerpos como: el bus se está moviendo hacia la derecha (alejándose del sistema de referencia) y el auto hacia la izquierda (acercándose al sistema de referencia).
2. Si ubicamos el sistema de referencia en un punto móvil, por ejemplo, el bus diríamos que el semáforo se está moviendo hacia la izquierda (alejándose) mientras que el auto se mueve hacia la izquierda (acercándose)
3. Si el sistema lo ubicamos en el perro que está parado junto al semáforo (el observador) diríamos: el semáforo no se mueve, el bus se mueve hacia la derecha y el auto se mueve hacia la izquierda.
Todas las descripciones que se han realizado sobre el movimiento son correctas y las diferencias entre ellas se deben al sistema de referencia con respecto al cual se realizó el estudio del movimiento. Es por ello que al estudiar el comportamiento de los cuerpos el análisis o descripción realizada, dependerá del sistema de referencia con respecto al cual se realizó.
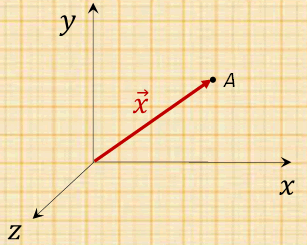
• Posición: se define como la ubicación de un cuerpo con respecto a un sistema de referencia. Matemáticamente, se representa por un vector que parte del origen del sistema de referencia hacia el punto donde se encuentra ubicado el cuerpo. La dimensión que corresponde a la posición es longitud, por lo tanto, su unidad en el sistema internacional (SI) es el metro (m). En la figura el vector \(\vec{x}\) representa la posición del punto A.
Autora
Escrito por Lismarihen Larreal para la Edición #104 de Enciclopedia Asigna, en 09/2021. Lismarihen es Ingeniera Mecánica, con maestría en Física Aplicada y doctorado en Ingeniería Ambiental, asímismo se desempeña como Docente e Investigadora en el Depto. de Física de la Facultad de Ingeniería de la Universidad del Zulia.