La interacción eléctrica entre partículas cargadas también puede expresarse en términos del campo eléctrico (\(\vec{E}\)). El campo eléctrico en un punto del espacio, es una cantidad vectorial que se define como la fuerza eléctrica (\(\vec{F}\)) que experimenta una carga de prueba \({{Q}_{0}}\) (considerada generalmente positiva), situada en ese punto, dividida entre la dicha carga, expresándose matemáticamente como: \(\vec{E}~=~\frac{{\vec{F}}}{{{Q}_{0}}}\) . Por su parte, las unidades del campo eléctrico se pautan en \({}^{N}\!\!\diagup\!\!{}_{C}\;\).
Imaginemos una habitación vacía en la cual ubicamos una carga puntual (carga de prueba). Podemos apreciar que ésta se mueve, dicho movimiento es consecuencia de la interacción de la carga de prueba con el medio que la rodea, es decir, de la fuerza eléctrica que experimenta. Esta interacción es producto del campo eléctrico generado por alguna carga o cuerpo cargado ubicado en el espacio que rodea a la carga de prueba.
Es importante destacar que el campo eléctrico en esta región del espacio existe independientemente de la existencia o no de la carga de prueba. De igual forma, la carga de prueba puede ser positiva o negativa, ya que el campo eléctrico en ese espectro no depende de la carga de prueba, sólo depende de la carga o sistema de carga que lo está generando.
Podemos decir entonces, que un campo eléctrico existe en una región del espacio, incluso en el vacío, si una carga de prueba, colocada en ese punto, experimenta una fuerza eléctrica.
Alrededor de todo cuerpo cargado existe un campo eléctrico generado por este, es decir, todo objeto cargado es una fuente de campo eléctrico. En este sentido resulta importante destacar que la carga de prueba también genera un campo eléctrico, pero como esta carga de prueba es tan pequeña, su efecto es despreciable, por lo que su presencia no afecta o modifica el campo eléctrico de la carga fuente (la que genera el campo eléctrico en la región del espacio).
Definición del vector campo eléctrico (\(\vec{E}\))
Se coloca una carga de prueba \({{Q}_{0}}\) en un punto P del espacio donde existe un campo eléctrico (\(\vec{E})\). La carga de prueba experimentará una fuerza eléctrica que dependerá de su valor \({{Q}_{0}}\), tal como lo establece la Ley de Coulomb (la fuerza eléctrica es proporcional a la carga).
Utilizando la Ley de Coulomb para determinar la fuerza eléctrica que experimenta la carga de prueba, tenemos que:
\(F~=~{{k}_{C}}~\frac{\left| Q \right|~\left| {{Q}_{0}} \right|}{{{r}^{2}}}\)
Sustituyendo esta fuerza eléctrica en la definición de campo eléctrico:
\(E~=\frac{F}{{{Q}_{0}}}~=~\frac{{{k}_{C}}~\frac{\left| Q \right|~\left| {{Q}_{0}} \right|}{{{r}^{2}}}}{{{Q}_{0}}}~={{k}_{C}}~\frac{\left| Q \right|}{{{r}^{2}}}\)
Esta es la expresión para calcular la magnitud del campo eléctrico generado por una carga puntual en cualquier punto del espacio. Se puede constatar a partir de la expresión anterior, que el campo eléctrico en una región del espacio es directamente proporcional a la magnitud de la carga que lo genera e inversamente proporcional al cuadrado de la distancia entre la carga y el punto.
Características en el campo eléctrico de una carga puntual
Una carga puntual positiva genera un vector campo eléctrico en dirección radial y dirigido hacia a fuera de ella, mientras que una carga puntual negativa genera un vector campo eléctrico en dirección radial, pero hacia dentro de ella, como se aprecia en la figura 1.
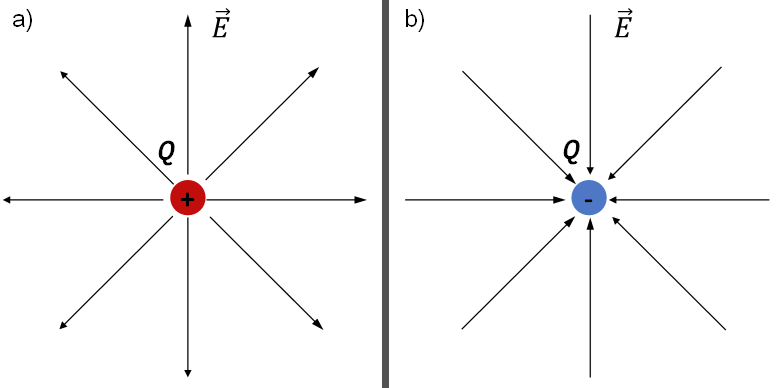
Figura 1. Representación del vector campo eléctrico (\(\vec{E}\)) generado por una carga puntual positiva a) y por una carga puntual negativa b).
Si se expresa la fuerza eléctrica en función del campo eléctrico, se tiene que:
\(\vec{F}~={{Q}_{0}}\vec{E}\)
Por lo tanto, la fuerza eléctrica que experimenta una carga puntual positiva tendrá la misma dirección y sentido que el campo eléctrico, mientras que la fuerza eléctrica que experimenta una carga puntual negativa tendrá la misma dirección pero sentido contrario al campo eléctrico, como se representa en la figura 2.
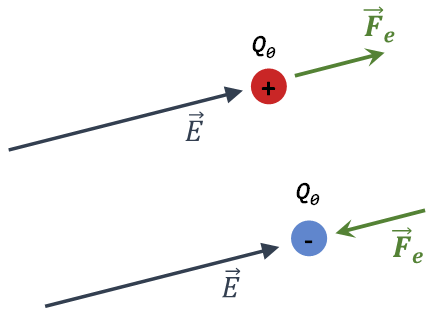
Figura 2. Fuerza eléctrica sobre una carga puntual situada en un campo eléctrico.
Características en el campo eléctrico de un conjunto de cargas puntuales
Si tenemos un conjunto de cargas puntuales, como las mostradas en la figura 3, el vector campo eléctrico total (\(\overrightarrow{{{E}_{T}}}\)) en un punto dado, será igual a la suma de los vectores campos eléctricos de cada una de las cargas (principio de superposición), excluyendo la carga de prueba, ejercen en el punto P. Este principio de superposición de \(\vec{E}\) se desprende del principio de superposición que se aplica a la fuerza eléctrica.
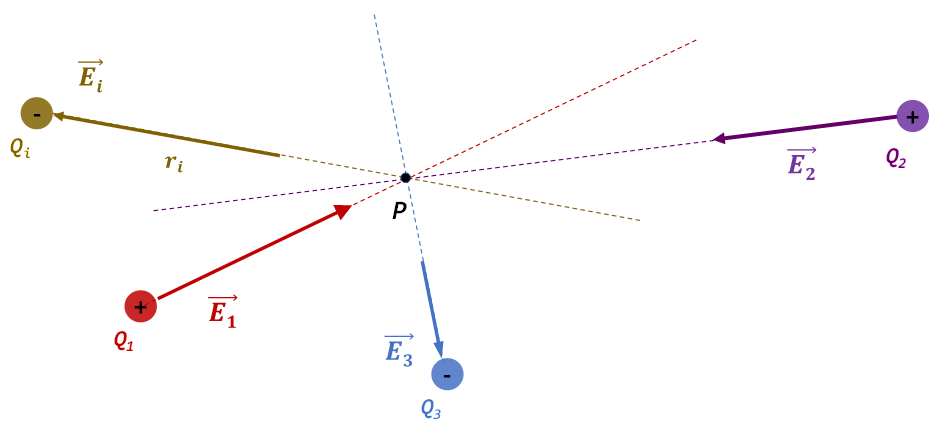
Figura 3. Campo eléctrico producido por un conjunto de cargas puntuales.
\(\overrightarrow{{{E}_{T}}}~=~{{k}_{C}}\underset{i~=1}{\overset{n}{\mathop \sum }}\,\frac{{{Q}_{i}}}{r_{i}^{2}}~{{\hat{r}}_{i}}\)
Donde \({{r}_{i}}\) es la distancia desde la i-ésima carga hasta el punto P donde se encuentra ubicada la carga de prueba \({{Q}_{0}}\), y \({{\hat{r}}_{i}}\) representa el vector unitario de \({{Q}_{i}}\) hacia P.
Autora
Escrito por Lismarihen Larreal para la Edición #103 de Enciclopedia Asigna, en 09/2021. Lismarihen es Ingeniera Mecánica, con maestría en Física Aplicada y doctorado en Ingeniería Ambiental, asímismo se desempeña como Docente e Investigadora en el Depto. de Física de la Facultad de Ingeniería de la Universidad del Zulia.