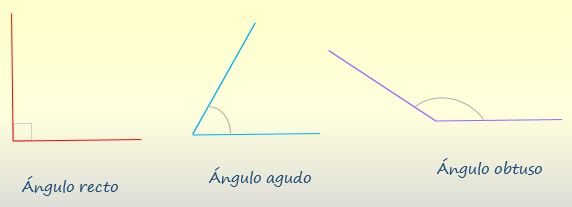
Primeramente, un ángulo está constituido por dos semirrectas que se encuentran en un punto al que se lo identifica como origen o vértice, trabajado dentro del espacio del plano. De acuerdo a las medidas, se diferencia entre 1. Ángulo recto, comprendiendo la figura que mide exactamente 90º; 2. Agudo es siempre menor que 90º; y 3. Obtuso, dentro de un espectro en el que supera los 90º y se mantiene debajo de los 180º. Las diferencias se pueden aprecian a nivel visual en la imagen que acompaña.
A la izquierda, en la imagen, está el ángulo recto, que suele diferenciarse a través de un cuadrado colocado en la esquina. El valor 90º casi nunca se escribe directamente, pero cuando aparece el cuadrado, se sabe de inmediato que se trata de un ángulo recto.
Otros ángulos se denotan con un arco, el ángulo agudo en el centro de la figura es, como indica su nombre, puntiagudo, mientras que la apertura del ángulo obtuso, en el dibujo a la derecha, es mayor y más amplia, pero no sobrepasa los 180º.
Ejemplos aplicados de ángulos
Los ángulos aparecen en infinidad de tamaños y formas, en todos los objetos cotidianos y no tan cotidianos, así como en personas, animales y plantas. Su medida es necesaria a la hora de construir adecuadamente edificaciones y cosas, e incluso en medicina, pues las articulaciones poseen determinadas posiciones en el espacio, dadas por ángulos.
Un ejemplo inmediato está en las letras mayúsculas del texto impreso. Algunas están compuestas de segmentos que forman diversos ángulos entre sí, como por ejemplo la letra “E”, con varios ángulos rectos, y la letra “A”, que tiene un ángulo agudo en el vértice.
Otro ejemplo destacado son las manecillas de los relojes de aguja, que forman distintos ángulos entre sí, según la hora.
En la siguiente imagen se observan más ejemplos de ángulos en objetos conocidos. El librero tiene esquinas en ángulo recto, que también se forman entre libros completamente verticales y el estante. Y si están inclinados, los libros forman ángulos con la superficie, agudos u obtusos, según la forma en que se elija medirlos.

Al abrir la computadora portátil, usualmente se forma un ángulo obtuso entre la pantalla y el teclado, o a veces un ángulo recto, según las preferencias del usuario.
Y como un ejemplo de su aparición en la geometría y la construcción, las pirámides contienen varios ángulos agudos en sus caras triangulares, uno de los cuales se ha destacado en la imagen.
Medida de ángulos
La medida de un ángulo se realiza con el transportador, un instrumento de forma circular o semicircular y graduado en grados sexagesimales, que surgen como resultado de dividir la circunferencia en 360 partes iguales. Cada una de las partes se denomina grado.
El transportador semicircular tiene una graduación que comienza en 0º y llega hasta 180º, mientras que el circular abarca la circunferencia completa, en total 360º.
Medir ángulos con un transportador es muy simple, solo hay que seguir estos pasos:
1. Colocar la marca del centro del transportador coincidiendo con el vértice del ángulo
3. Hacer coincidir el 0º del transportador con uno de los lados del ángulo.
5. Medir con el transportador la graduación del mismo que corresponde al otro lado del ángulo.
Otras medidas para los ángulos
Un ángulo central se determina al tomar como vértice el centro de una circunferencia de radio R. En ese caso, los lados del ángulo miden R, pero si además el arco correspondiente entre los lados también mide R, el ángulo formado mide 1 radián.
La medida en radianes de un ángulo central θ viene dada por el cociente entre el arco subtendido “s” y el radio R de la circunferencia:
\(\theta =\frac{s}{R}\)
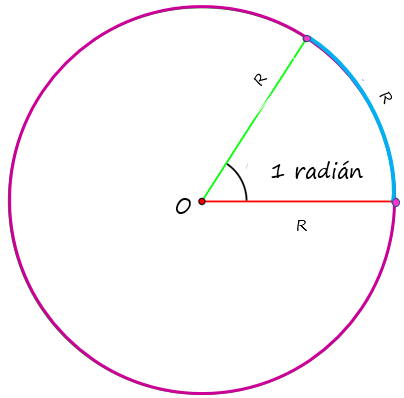
Suponiendo que la línea naranja en la figura se deja fija, y la línea verde se puede mover por toda la circunferencia en sentido antihorario (también horario, si se prefiere), cuando se da una vuelta completa, ambas líneas coinciden, pero la línea verde habrá girado 360º. Entonces la longitud del arco, o contorno, es igual a la longitud de la circunferencia, que es 2πR. De esta manera el ángulo girado, en radianes, es:
\(\theta =\frac{{2\pi R}}{R}=2\pi \)
De allí se sigue que 360º = 2π radianes.
En vista de que el ángulo recto es la cuarta parte de de 360º, ya que 360 ÷ 4 = 90, en radianes el ángulo recto es 2π ÷ 4 = π / 2, que se lee “pi medio radianes” o simplemente “pi medio”.
Se siguen entonces que un ángulo agudo estará comprendido entre 0 y π/2, mientras que un ángulo obtuso lo está entre π/2 y π.
Colocar en práctica
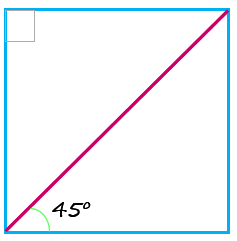
¿Cuánto mide el ángulo entre la diagonal del cuadrado y uno de sus lados, tanto en grados como en radianes?
Respuesta
Tomando una esquina arbitraria del cuadrado, en el interior del mismo, se forma un ángulo de 90º = π/2. La diagonal del cuadrado biseca este ángulo (lo divide en dos partes iguales), de esta manera, el ángulo entre la diagonal y un lado cualquiera es 45º = π/4.
