El pentágono es una figura geométrica plana, formada por 5 segmentos de recta, llamados lados, que se cierran para conformar la figura. Pertenece a la familia de los polígonos y su nombre deriva del griego pentágōnos, a partir de pente, que remite a cinco, y -gōno, de gōnía, que hace referencia a ángulo.
En efecto, el pentágono posee 5 ángulos internos y otros tantos ángulos externos, cuyos vértices coinciden con las 5 puntas del pentágono. Y, al igual que otros polígonos, el pentágono se utiliza en logotipos, arquitectura y creación y diseño de numerosos objetos de ornato.
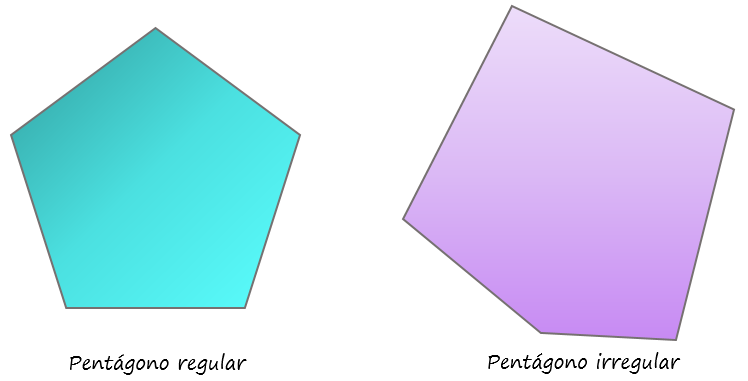
La siguiente figura muestra dos pentágonos, el de la izquierda se denomina pentágono regular, pues sus cinco lados y ángulos internos tienen igual medida, es decir, es equilátero y equiángulo. Cada ángulo interno del pentágono regular mide 108º.
Por el contrario, el pentágono de la derecha es irregular, ya que sus lados y ángulos internos son diferentes.
Principales elementos de un pentágono
En cualquier pentágono, sea regular o no, se distinguen los siguientes elementos:
• Lados, son los 5 segmentos que, al cerrarse, conforman la figura.
• Vértices, son los puntos en común entre los lados, a modo de esquinas. El pentágono tiene 5 vértices.
• Ángulo interno, es el que se encuentra entre dos lados adyacentes. La suma de los ángulos internos de cualquier pentágono es igual a 540º. Y si este es regular, cada ángulo interno mide 108º.
• Ángulo externo, se crea entre un lado cualquiera y la prolongación de uno de los lados adyacentes. Para un pentágono regular, este ángulo mide siempre 72º. La suma del ángulo interno y el ángulo externo es 108º + 72º = 180º.
• Diagonales, segmentos que conectan dos vértices no consecutivos. El número de diagonales D de un polígono, depende del número de lados “n” que tenga, y se calcula a través de:
\(D=\frac{{n\left( {n-3} \right)}}{2}\)
Como n = 5 para el pentágono, este tiene en total:
\(D=\frac{{5\left( {5-3} \right)}}{2}=5~diagonales\)
Para el pentágono regular, se definen adicionalmente los siguientes segmentos:
• Apotema, es el segmento de menor longitud que une el centro con uno de los lados. Llamando \({{L}_{{ap}}}\) a la medida de la apotema, para un pentágono de lado ℓ, se calcula como:
\({{L}_{{ap}}}=\frac{\ell }{2}\cdot \sqrt{{1+\frac{2}{{\sqrt{5}}}}}\)
• Radio, denotado como “r”, es el segmento que une un vértice con el centro.
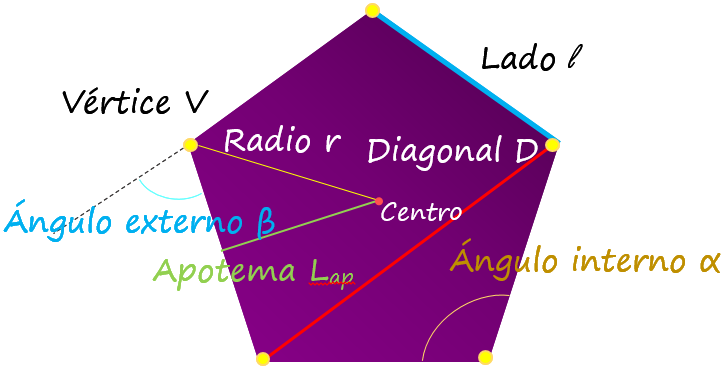
La figura a continuación muestra cómo son estos elementos en un pentágono regular.
Clasificación de los pentágonos
Los pentágonos, como cualquier otro polígono, se clasifican atendiendo a la longitud de sus lados o la medida de sus ángulos. Tal como se explicó anteriormente, los pentágonos pueden ser:
• Regulares, si todos sus lados y ángulos internos tienen igual medida. Nótese que el pentágono regular posee ejes de simetría. Se puede trazar uno de ellos al unir un vértice con el centro, quedando dos mitades que son reflejo especular una de la otra.
• Irregulares, son aquellos cuyos lados y/o ángulos internos poseen diferentes medidas.
En atención a los ángulos internos, los pentágonos también pueden ser:
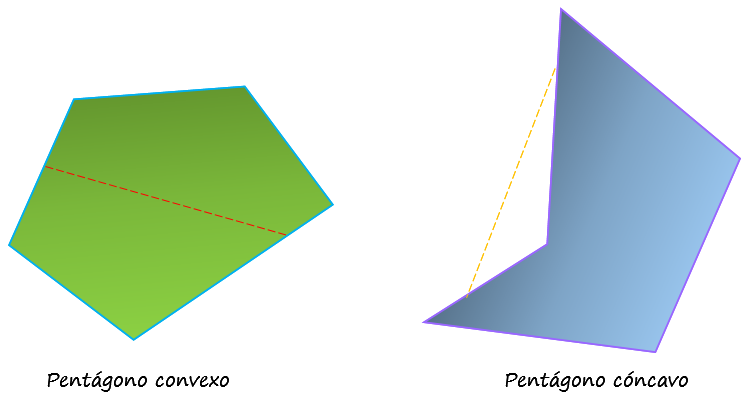
• Convexos, aquellos cuyos ángulos internos miden entre 0 y 180º (pueden ser regulares o irregulares), como los pentágonos de las figuras anteriores. Todo segmento que une dos puntos de lados diferentes del pentágono convexo, es interior a la figura.
• Cóncavos, cuando tienen al menos un ángulo interno mayor a 180º. Al unir dos puntos del pentágono cóncavo mediante un segmento, parte de este puede quedar por fuera de la figura.
Cómo calcular el perímetro de un pentágono
El perímetro P es la medida del contorno del pentágono y se calcula de la siguiente manera:
Pentágono regular
P = 5ℓ
Donde ℓ es la longitud del lado.
Pentágono irregular
Corresponde a la suma de la longitud de cada lado.
P = ℓ1 + ℓ2 + ℓ3 + ℓ4 + ℓ5
Área de un pentágono
De nuevo, el cálculo del área A depende de si el pentágono es o no regular.
Pentágono regular
Existen varias maneras de calcular el área A del pentágono regular, según los datos disponibles:
Área en función del lado ℓ
\(A=\frac{{5{{\ell }^{2}}}}{4}\cdot cot\frac{\pi }{5}\)
Área en función de la apotema Lap
\(A=5L_{{ap}}^{2}\cdot \sqrt{{5-2\sqrt{5}}}\)
Área en función de la apotema Lap y el perímetro P
\(A=\frac{1}{2}{{L}_{{ap}}}\cdot P\)
Pentágono irregular
Para el área del pentágono irregular no existe una fórmula única, sin embargo, es posible encontrar el área dividiendo la figura en cinco triángulos, calculando el área de cada uno y sumando los resultados. Cada lado del pentágono coincide con un lado de uno de los triángulos, y todos estos confluyen en un vértice común.
Ejemplo resuelto
Calcular perímetro y área de un pentágono regular, cuya apotema mide 4.0 pulgadas y la longitud del lado es igual a 5.8 pulgadas.
Respuesta
Se utilizan las fórmulas dadas anteriormente para un pentágono regular, con ℓ = 5.8 pulgadas y
\({{L}_{{ap}}}=4.0~pulgadas\):
P = 5ℓ = 5×5.8 pulgadas = 29 pulgadas
\(A=\frac{1}{2}{{L}_{{ap}}}\cdot P=0.5\times 4.0~pulgadas~\times 29~pulgadas=58~pulgada{{s}^{2}}\)
