Los vectores son la herramienta que se utiliza para representar las cantidades físicas vectoriales, es decir, aquellas que, además de una magnitud, poseen dirección y sentido (orientación espacial). Como ejemplos de estas cantidades vectoriales tenemos: el desplazamiento, la velocidad, así como también la fuerza y aceleración, entre otras. Los vectores se representan por letras mayúsculas sobre la cual se dibuja una flecha (\(\vec{A}\)).
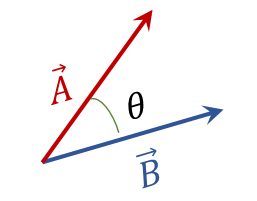
Elementos de un vector
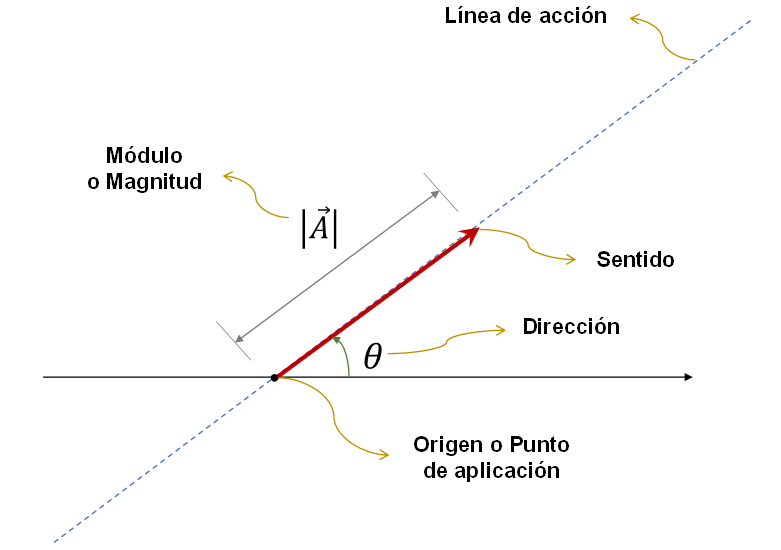
Figura 1. Elementos que caracterizan a un vector.
• El origen o punto de aplicación de un vector, es el punto en el cual se encuentra aplicado o está actuando el vector.
• Línea de acción, es la línea infinita que nos indica la dirección en la cual se encuentra el vector.
• El módulo o magnitud, es un número real o cantidad escalar que representa la longitud del mismo, es decir, la distancia entre su origen y su extremo o punta. La magnitud de un vector se expresa como: \(\left| {\vec{A}} \right|\) ó \(A\).
• Dirección, representa el ángulo \(\theta \) que forma el vector con el respecto al eje horizontal positivo, medido en sentido contrario a las agujas del reloj.
• Sentido, está representado por la punta de la flecha del vector y se encuentra relacionado con la dirección del mismo.
Tipos de vectores
a) Vector fijo: es aquel que tiene un punto de aplicación u origen fijo, es decir, su efecto sobre el objeto está asociado al punto de aplicación.
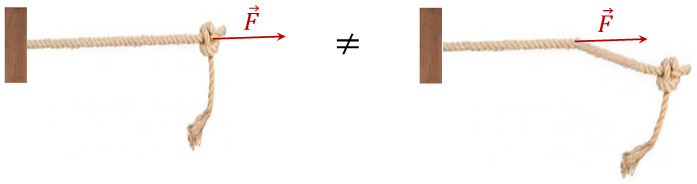
b) Vector deslizante: puede ser aplicado en cualquier punto a lo largo de su línea de acción.
c) Vector libre: puede ubicarse en cualquier lugar del espacio.
d) Vector negativo u opuesto: es un vector que tiene la misma magnitud y dirección, pero sentido contrario a un vector dado.
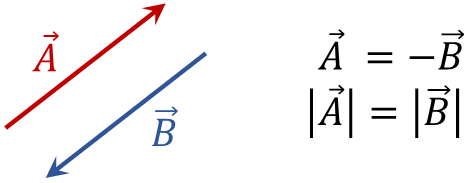
e) Vector unitario: es un vector cuya magnitud es igual a la unidad, es adimensional (sin dimensiones) y que se emplea para indicar la dirección de un vector dado. Los vectores unitarios más utilizados son: \(\hat{i}~,~\hat{j}~,~\hat{k}\) que se emplean para indicar la dirección y sentido de los ejes coordenados \(x,~y,~z\), respectivamente.
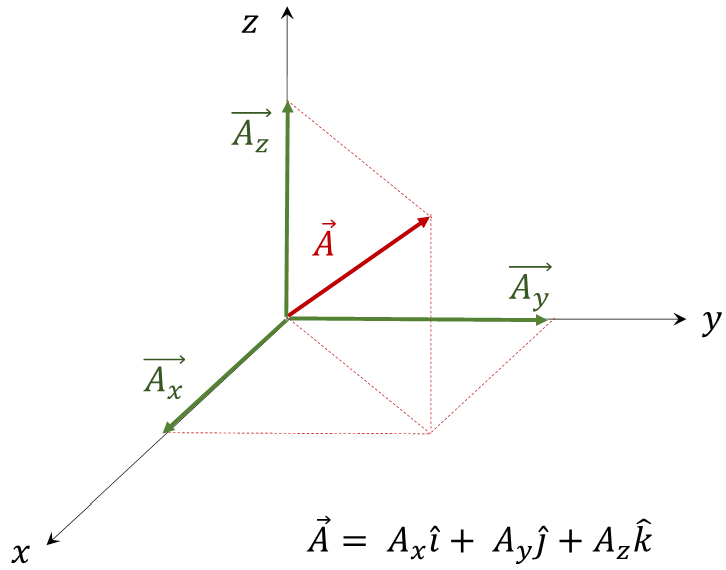
Se puede calcular el vector unitario de cualquier vector dado como el cociente entre el vector y su magnitud, es decir:
• \(\hat{A}~=~\frac{{\vec{A}}}{\left| {\vec{A}} \right|}\)
Operaciones con vectores
a) Suma algebraica de vectores
Para sumar algebraicamente (sumar o restar) dos o más vectores debemos sumar algebraicamente cada una de sus componentes \(x,~y,~z\). Esta suma algebraica cumple con las siguientes propiedades:
• Conmutativa: \(\vec{A}+~\vec{B}~=~\vec{B}~+\vec{A}\)
• Asociativa: \(\vec{A}+\left( \vec{B}+~\vec{C} \right)=\left( \vec{A}+~\vec{B} \right)+\vec{C}~=~\left( \vec{A}+~\vec{C}~ \right)+~\vec{B}\)
• Distributiva vectorial: \(m~\left( \vec{A}+~\vec{B} \right)~=m~\vec{A}+m\vec{B}\)
• Distributiva escalar: \(\vec{A}~\left( m+n \right)=~m~\vec{A}+n~\vec{A}~\)
b) Multiplicación escalar de vectores
La multiplicación escalar o producto punto de dos vectores se define como:
• \(\vec{A}\cdot \vec{B}~=~\left| \vec{A}~ \right|~\left| {\vec{B}} \right|cos\theta \)
Donde, \(\theta \) es el menor ángulo comprendido entre ambos vectores, es decir, \(0{}^\circ ~\le ~\theta ~\le 180{}^\circ \). El resultado del producto punto de dos vectores en un escalar (un número).
Dado los vectores \(\vec{A}~=~{{A}_{x}}~\hat{i}+~~{{A}_{y}}~\hat{j}+~{{A}_{z}}~\hat{k}\) y \(\vec{B}~=~{{B}_{x}}~\hat{i}+~~{{B}_{y}}~\hat{j}+~{{B}_{z}}~\hat{k}\), también puede definirse en producto escalar entre ellos como:
\(\vec{A}\cdot \vec{B}=~{{A}_{x}}~{{B}_{x}}+~~{{A}_{y}}~{{B}_{y}}+~{{A}_{z}}~{{B}_{z}}\) = cantidad escalar
Algunas propiedades el producto escalar o producto punto son:
• \(\vec{A}\cdot \vec{B}~=~\vec{B}\cdot ~\vec{A}~\)
• \(\vec{A}\cdot \left( \vec{B}+~\vec{C} \right)=~\vec{A}\cdot \vec{B}+~\vec{A}\cdot \vec{C}\)
• Si \(\vec{A}~\ne ~\vec{0}\) , \(\vec{B}~\ne ~\vec{0}\) , \(\vec{A}\cdot \vec{B}~=~\vec{0}~\) entonces \(\vec{A}~\) Ʇ \(~\vec{B}\).
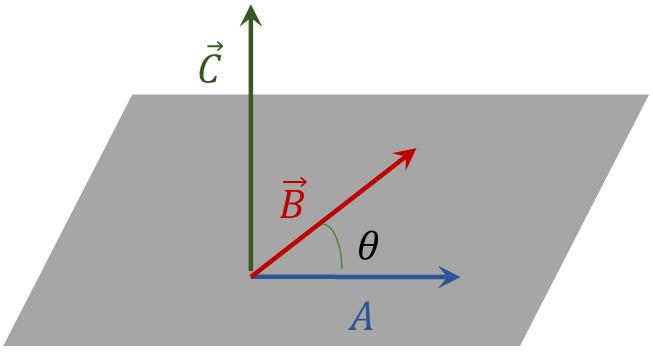
c) Multiplicación vectorial de vectores
Por definición, la multiplicación vectorial o producto cruz de dos vectores \(\vec{A}~\) y \(~\vec{B}\) se define como:
• \(\vec{A}~\times ~\vec{B}~=~\vec{C}\)
Cuya magnitud está dada por:
• \(\left| \vec{A}~\times ~\vec{B} \right|~=~\left| \vec{A}~ \right|~\left| {\vec{B}} \right|sen~\theta \)
Donde, \(\theta \) es el menor ángulo comprendido entre ambos vectores, es decir, \(0{}^\circ ~\le ~\theta ~\le 180{}^\circ \). El resultado del producto vectorial de dos vectores en un vector perpendicular al plano formado por los vectores \(\vec{A}~\) y \(~\vec{B}\).
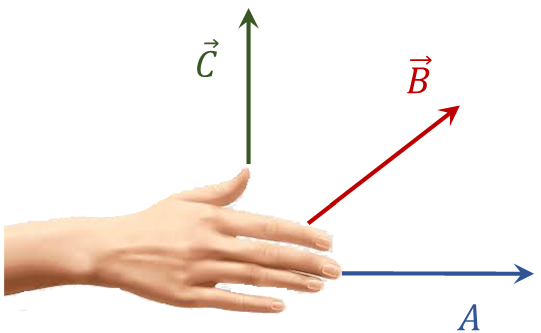
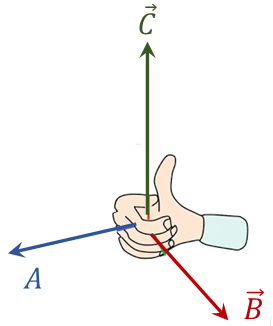
Para realizar el producto vectorial o producto cruz de dos vectores \(\left| \vec{A}~\times ~\vec{B} \right|\), utilizamos la regla de la mano derecha, es decir, colocamos la palma de la mano derecha con los dedos en la dirección del primer vector que deseamos multiplicar (\(\vec{A}~\)) y al cerrar la palma hacemos el recorrido de llevar el vector \(\vec{A}~\) hacia el \(\vec{B}\), el dedo pulgar nos indicará la dirección del vector resultante, es decir, \(\vec{C}\).
Algunas propiedades importantes del producto vectorial o producto cruz son:
• \(\vec{A}~\times ~\vec{B}~=~-~\vec{B}~\times ~~\vec{A}~\)
• \(\vec{A}~\times \left( \vec{B}+~\vec{C} \right)=~\vec{A}~\times ~\vec{B}+~\vec{A}~\times ~\vec{C}\)
• Si \(\vec{A}~\ne ~\vec{0}\) , \(\vec{B}~\ne ~\vec{0}\) , \(\vec{A}~\times ~\vec{B}~=~\vec{0}~\) entonces \(\overrightarrow{A~}~\) // \(~\vec{B}\).
Por ejemplo
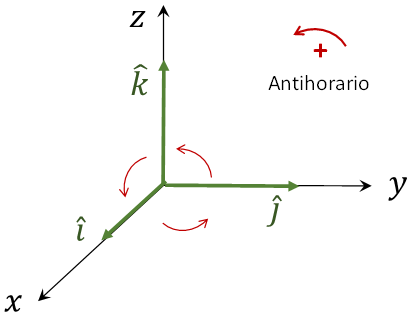
\(\hat{i}~\times ~\hat{j}~=~\hat{k}~~\), \(~\hat{j}~\times ~\hat{k}~=~\hat{i}\) , \(~\hat{k}~\times ~\hat{i}~=~\hat{j}\)
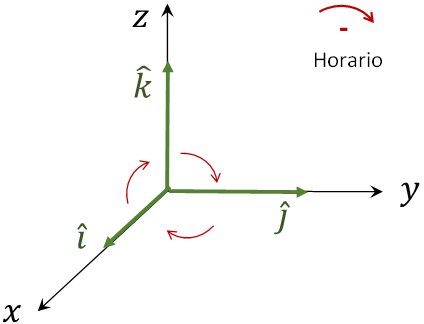
\(~~\hat{j}\times ~\hat{i}=~-\hat{k}~~\), \(\hat{k}~\times ~\hat{j}~~=~-\hat{i}\) , \(\hat{i}~\times \hat{k}~~~=~-\hat{j}\)
Autora
Escrito por Lismarihen Larreal para la Edición #104 de Enciclopedia Asigna, en 09/2021. Lismarihen es Ingeniera Mecánica, con maestría en Física Aplicada y doctorado en Ingeniería Ambiental, asímismo se desempeña como Docente e Investigadora en el Depto. de Física de la Facultad de Ingeniería de la Universidad del Zulia.