El trabajo y la energía cinética son dos magnitudes físicas estrechamente relacionadas, a partir de lo que se observa que el trabajo hecho por una fuerza neta respecto del movimiento de un cuerpo entre una posición inicial P1 y otra final P2 sobre una trayectoria acarrea un cambio de energía cinética, formulándose matemáticamente en:
\({{W}_{{neto}}}=\text{ }\!\!\Delta\!\!\text{ }K\) .
En esta ecuación, \({{W}_{{neto}}}~\) representa el trabajo hecho por todas las fuerzas que actúan sobre el cuerpo, y ΔK es la variación en la energía cinética K, dada por: \(\text{ }\!\!\Delta\!\!\text{ }K={{K}_{{final}}}-{{K}_{{inicial}}}\)
El trabajo realizado por toda fuerza conservativa o no conservativa siempre será igual al cambio de energía cinética del cuerpo o sistema. Si el sistema aumenta su rapidez (la velocidad en el punto final es mayor que en el punto inicial) el trabajo será positivo, mientras que si el sistema pierde rapidez (la velocidad en el punto final es menor que en el punto inicial) el trabajo será negativo.
Cuando en un sistema sólo intervienen fuerzas conservativas, se dice que la energía mecánica del sistema (suma de la energía potencial y cinética) se conserva, es decir, la energía mecánica inicial y final del sistema son iguales.
\(~{{E}_{f}}={{E}_{i}}~\Rightarrow ~{{k}_{f}}+~{{U}_{f}}={{k}_{i}}+~{{U}_{i}}\)
Dado que existe una conexión directa entre ambas magnitudes, las unidades del trabajo y la energía cinética son las mismas: el joule, abreviado J, en el Sistema Internacional de Unidades SI.
En el teorema se establece claramente cómo es el efecto cinemático que tienen las fuerzas sobre el objeto. Es un hecho que se aprecia fácilmente al jugar cualquier deporte de balón, pues se necesita el trabajo de una fuerza, a través del pie, la cabeza o algún instrumento, para que el balón sea impulsado con mayor rapidez hacia otro compañero o al área rival.
Y no solamente se requiere trabajo para hacer que un objeto se mueva más de prisa, también hace falta para detenerlo. Aumentar la rapidez o frenar, son cambios cinemáticos que se producen gracias al trabajo de alguna fuerza.
La ventaja de este teorema es que relaciona dos cantidades escalares, y su carácter es general, ya que es válido tanto para un movimiento rectilíneo, como para otro curvilíneo, para fuerzas constantes y fuerzas variables. No es preciso, por lo tanto, especificar direcciones y sentido, como sucede al trabajar directamente con vectores.
Al teorema trabajo-energía cinética se le conoce también como principio del trabajo y la energía.
El efecto de los signos del trabajo
El trabajo neto puede ser positivo, negativo o cero. En tal caso, sus efectos sobre el movimiento son los siguientes:
• \({{W}_{{neto}}}>0\), significa que \(\text{ }\!\!\Delta\!\!\text{ }K\) también es positivo, y por lo tanto \({{K}_{{final}}}\) es mayor que \({{K}_{{inicial}}}\), incrementándose la rapidez del objeto.
• \({{W}_{{neto}}}<0\), implica que \(\text{ }\!\!\Delta\!\!\text{ }K\) es negativo, en tal caso \({{K}_{{final}}}\) es menor que \({{K}_{{inicial}}}\) y la rapidez del objeto disminuye. • \({{W}_{{neto}}}=0\), por lo tanto \(\text{ }\!\!\Delta\!\!\text{ }K=0\) , lo cual significa que la energía cinética del objeto no cambia, se mantiene constante. El teorema también funciona en sentido inverso: si \(\text{ }\!\!\Delta\!\!\text{ }K\) es positivo, el trabajo neto también lo es. Si \(\text{ }\!\!\Delta\!\!\text{ }K\) es negativo, el trabajo neto es negativo. Y por último, si \(\text{ }\!\!\Delta\!\!\text{ }K=0\), el trabajo neto es 0.
Ejemplos de aplicación
Trabajo neto positivo
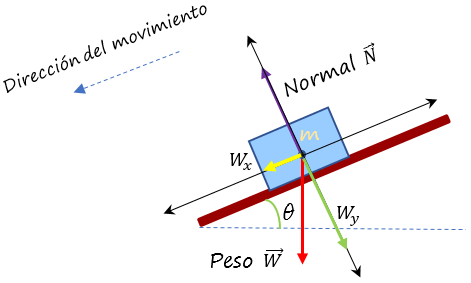
Supóngase que se coloca un objeto en lo alto de un plano inclinado muy pulimentado. El objeto es liberado y de inmediato desliza cuesta abajo.
La componente del peso paralela al plano inclinado \({{W}_{x}}~\) no está equlibrada por ninguna otra fuerza, según se ve en el diagrama de cuerpo libre adjunto, por lo tanto, proporciona una aceleración en esa misma dirección, haciendo que el objeto vaya cada vez más rápido, aumentando su energía cinética.
Por su parte, la fuerza normal \(\vec{N}\) y la componente del peso perpendicular al plano
\({{W}_{y}}\), no hacen trabajo, por ser perpendiculares a la dirección del movimiento.
Trabajo neto negativo
Se le proporciona un breve impulso a un objeto colocado sobre una superficie rugosa horizontal, dejándolo en libertad.
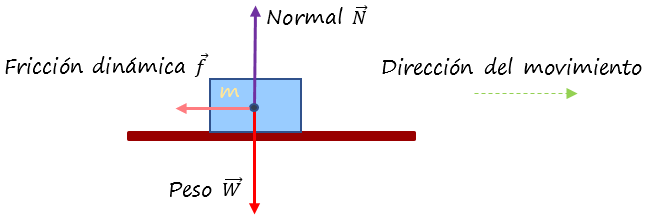
El objeto se detendrá luego de recorrer una cierta distancia, ya que la única fuerza no equilibrada es la fricción dinámica, la cual es paralela al movimiento, pero cuyo sentido es contrario siempre.
Las fuerzas que son paralelas, pero contrarias al movimiento, hacen trabajo negativo sobre el cuerpo, reduciendo su energía cinética.
Trabajo neto nulo
El trabajo neto sobre un objeto puede ser nulo y, sin embargo, esto no significa necesariamente ausencia de fuerzas sobre el cuerpo, o que esté en reposo.
Por ejemplo, en el movimiento circular uniforme MCU hay una fuerza centrípeta, encargada de mantener el objeto dando vueltas. Esta fuerza no hace un trabajo desde el punto de vista físico, pues es perpendicular al desplazamiento.
Un ejemplo de esta situación es el giro de una piedra atada a una cuerda, recorriendo circunferencias paralelas al plano del suelo con rapidez constante. En este caso, la tensión en la cuerda proporciona la fuerza centrípeta.
Esta fuerza no cambia la energía cinética del objeto, ya que su rapidez siempre es la misma, al menos mientras se mueve con MCU, pero sí proporciona la aceleración centrípeta, que modifica continuamente la dirección del vector velocidad.
Y siempre que un objeto se mueve con rapidez constante, su energía cinética se mantiene constante también, por lo que \(\text{ }\!\!\Delta\!\!\text{ }K=0\).
Ejemplo numérico
Es muy fácil aplicar el teorema, por ejemplo ¿cuánto trabajo se hace al acelerar un automóvil de 1200 kg para que vaya desde 25 m/s (90 km/h) hasta 33 m/s (aproximadamente 120 km/h)?
El teorema trabajo-energía cinética asegura que:
\({{W}_{{neto}}}=\text{ }\!\!\Delta\!\!\text{ }K={{K}_{{final}}}-{{K}_{{inicial}}}\)
Como la energía cinética es:
\(K=~\frac{1}{2}m{{v}^{2}}\)
Con m igual a la masa del objeto, entonces, sustituyendo valores en el teorema, resulta:
\({{W}_{{neto}}}={{K}_{{final}}}-{{K}_{{inicial}}}=\frac{1}{2}mv_{{final}}^{2}-\frac{1}{2}mv_{{inicial}}^{2}=\left( {0.5\times 1200\times {{{33}}^{2}}-0.5\times 1200\times {{{25}}^{2}}} \right)~J=278400~J\)
Autora
 Escrito por Lismarihen Larreal para la Edición #102 de Enciclopedia Asigna, en 08/2021. Lismarihen es Ingeniera Mecánica, con maestría en Física Aplicada y doctorado en Ingeniería Ambiental, asímismo se desempeña como Docente e Investigadora en el Depto. de Física de la Facultad de Ingeniería de la Universidad del Zulia.
Escrito por Lismarihen Larreal para la Edición #102 de Enciclopedia Asigna, en 08/2021. Lismarihen es Ingeniera Mecánica, con maestría en Física Aplicada y doctorado en Ingeniería Ambiental, asímismo se desempeña como Docente e Investigadora en el Depto. de Física de la Facultad de Ingeniería de la Universidad del Zulia.