La interferencia de ondas consiste en la combinación o solapamiento de ondas en una misma región del espacio, dando como resultado un patrón de interferencia, tras lo cual prosiguen su camino sin alteración. Se trata de una cualidad muy particular de las ondas, que las hace distinguirse de las partículas con masa, las cuales, al menos a nivel macroscópico, no pueden compartir el mismo espacio a la vez.
Durante la interferencia se producen diversos fenómenos, en los que las ondas se combinan para dar como resultado una onda de mayor o menor amplitud, o tal vez, cancelarse definitivamente.
Las ondas de todo tipo, luminosas, sonoras, electromagnéticas, las que se forman en el agua y más, son capaces de interferir y combinarse, dando lugar a diferentes patrones de interferencia.
Diferencia entre interferencia constructiva y destructiva
Las ondas cumplen el principio de superposición, el cual indica cómo es la onda combinada. El principio afirma que cuando dos o más ondas ocupan el mismo espacio a la vez, los desplazamientos de cada una, por separado, se suman en cada punto de dicha región y dan como resultado un desplazamiento neto.
De esta manera se produce una onda de amplitud mayor, menor o nula, dependiendo de la forma en que se superpongan las ondas.
Constructiva: Al solaparse la cresta de una onda con la cresta de otra, el resultado es una onda de mayor amplitud. A este efecto se lo conoce como interferencia constructiva y se dice entonces que las ondas están en fase (véase la descripción matemática de la interferencia, más adelante).
Destructiva: En cambio, si se encuentra la cresta de una onda con el valle de otra, las respectivas amplitudes se cancelan en cierta medida, dando como resultado una disminución de la amplitud de la onda resultante, o la anulación completa, llamada interferencia destructiva total. Sin embargo, esto no debe interpretarse como que la energía desaparece por completo, ya que las partículas del medio continúan oscilando, por lo que disponen de energía cinética.
Ejemplos de interferencia de ondas
El eco
Una de las manifestaciones más frecuentes del fenómeno de la interferencia de ondas es el eco. Al emitir un grito dirigido a una pared o un acantilado que está al frente, la onda sonora se refleja de vuelta sobre la superficie rígida y se traslapa con la onda emitida inicialmente, dando como resultado el eco.
Ondas en un estanque
Cuando se lanzan dos piedras simultáneamente a un estanque, se forman dos conjuntos de ondas circulares que interfieren. Las crestas (o los valles) se traslapan en algunas regiones, ocurriendo entonces la interferencia constructiva, por lo que las partículas de agua oscilan allí con una mayor amplitud.
En cambio, en otras zonas se encuentran las crestas con valles, dando lugar a interferencia destructiva, donde el agua carece de movimiento de arriba abajo.
Finalmente, hay regiones intermedias, en las cuales se produce interferencia destructiva parcial (interferencia constructiva parcial, si se prefiere). Cuando las amplitudes de las ondas que interfieren son diferentes, la interferencia nunca es completamente destructiva.
El silenciador del automóvil
En un automóvil, los gases producidos en el motor van de una presión elevada dentro de los cilindros a la presión atmosférica, a la salida del tubo de escape, lo que normalmente produce bastante ruido.
Para evitarlo, se añade un dispositivo llamado silenciador, que consiste en un tubo con cámaras en su interior, en las cuales el sonido se refleja en uno y otro sentido, produciendo interferencia destructiva que disminuye su amplitud, y con ella la intensidad de la onda sonora.
Descripción matemática de la interferencia
Con el fin de demostrar cómo se produce la interferencia, se considera el caso más simple de dos ondas sinusoidales \({{y}_{1}}\) y \({{y}_{2}}\) con idéntica amplitud A, frecuencia ω, número de onda k y una diferencia de fase φ, como podrían ser las que se propagan a lo largo de una cuerda tensa:
y1= A sen (kx-ωt)
y2 = A sen (kx-ωt + φ)
En ambas ondas, “t” representa el tiempo y “x” es la posición. A la onda resultante se la llama \({{y}_{R}}\) y es la suma de \({{y}_{1}}~\) y \({{y}_{2}}\) :
\({{y}_{R}}=~{{y}_{1}}+{{y}_{{2~}}}=A~sen~\left( {kx-\omega t} \right)+A~sen~\left( {kx-\omega t+\phi } \right)\)
Para efectuar la suma de estas ondas, es de gran ayuda la siguiente identidad trigonométrica:
\(sen~\alpha +sen~\beta =2\cdot sen~\left( {\frac{{\alpha +\beta }}{2}} \right)\cdot cos~\left( {\frac{{\alpha -\beta }}{2}} \right)\)
Por lo tanto:
\({{y}_{R}}=2A\cdot sen~\left( {\frac{{2kx-2\omega t+\phi }}{2}} \right)\cdot cos~\left( {\frac{\phi }{2}} \right)~\)
Que se reescribe como:
\({{y}_{R}}=\left[ {2A\cdot cos~\left( {\frac{\phi }{2}} \right)~} \right]\cdot sen~\left( {\frac{{2kx-2\omega t+\phi }}{2}} \right)\)
Esta onda resultante también es sinusoidal, pero su amplitud resultante, llamada \({{A}_{R}}\), es:
\({{A}_{R}}=2A\cdot cos~\left( {\frac{\phi }{2}} \right)\)
Lo cual significa que depende del ángulo de fase de las ondas que interfieren.
Cuando \(cos~\left( {\frac{\phi }{2}} \right)=1\), el valor de \({{A}_{R}}\) es máximo, en ese caso φ = 0, lo que significa que las crestas y los valles de las ondas están completamente alineados. En ese caso, la amplitud resultante es el doble de las amplitudes de las ondas participantes, y se tiene interferencia constructiva:
\({{A}_{R}}=2A\)
Gráficamente:
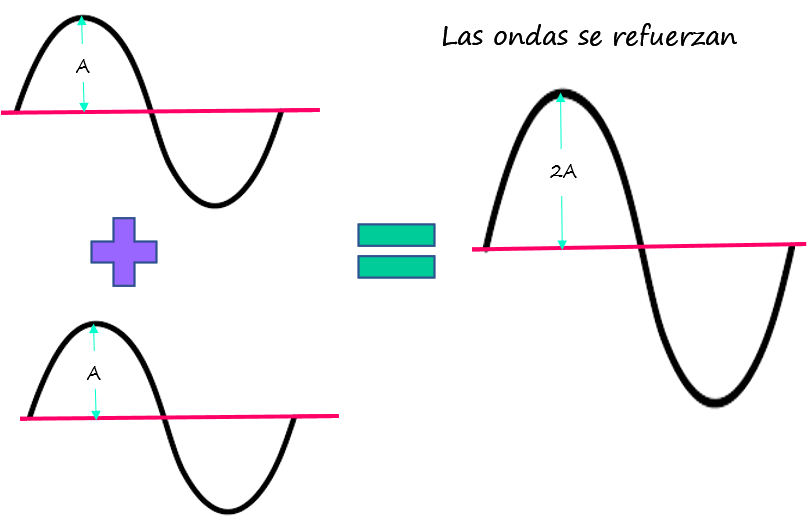
En cambio, cuando φ = ± π, entonces \(cos~\left( {\frac{\phi }{2}} \right)=0\) y las ondas están fuera de fase, produciendo interferencia destructiva, ya que la cresta de onda se alinea con el valle de la otra, dando como resultado una amplitud cero.
También se da este caso siempre que φ sea de la forma ± kπ, siendo k impar, por ejemplo ± π, ± 3π, ± 5π…
